Comète de Goldbach

La comète de Goldbach[1] est le nom donné à un tracé de la fonction $g(E)$ , que l'on appelle fonction de Goldbach. La fonction de Goldbach est étudiée en relation avec la conjecture de Goldbach. La fonction $g(E)$ est défini pour tous les entiers pairs $E>2$ pour être le nombre de façons différentes dans laquelle E peut être exprimée comme la somme de deux nombres premiers. Par exemple, $g(22)=3$ car 22 peut être exprimée comme la somme de deux nombres premiers de trois manières différentes ( $22=11+11=5+17=3+19$ ).

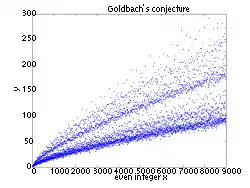
Anatomie de la Comète de Goldbach

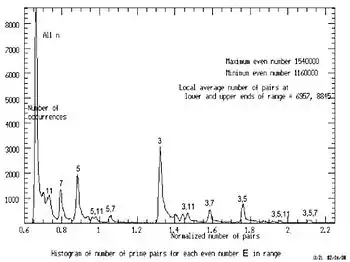
Un moyen de présenter les données de la comète est sous forme d'histogramme. La fonction $g(E)$ peut être normalisée en divisant par la valeur localement moyenne de g, g_av, en prenant environ 1000 valeurs avoisinant le nombre pair E. L'histogramme peut alors être accumulé sur une plage allant jusqu'à environ 10 % de chaque côté de centrale E.

Un tel histogramme apparaît à droite. Une série de pics bien définis est évidente. Chacune de ces pics peut être identifiée comme étant formée par un ensemble de valeurs de $E/2$ , qui ont des plus petits facteurs. Les principaux pics correspondent aux facteurs les plus bas de 3, 5, 7... comme représenté plus haut.

Il existe une hiérarchie de pics; les pics principaux sont composés de pics subsidiaires, avec une succession de seconds plus petits facteurs de $E/2$ . Cette hiérarchie se poursuit jusqu'à ce que tous les facteurs sont épuisés.

La section agrandie montre la succession de pics subsidiaires plus en détail.

La position relative des pics résulte de la forme développée par Hardy et Littlewood:[2]

{\frac {g(E)}{g_{av}}}=\Pi _{2}\prod {\frac {(p-1)}{(p-2)}}\,,\quad \quad \quad \quad \quad \quad (1)

où le produit est pris sur l'ensemble des nombres premiers p qui sont des facteurs de $E/2$ . Le facteur sur la droite est la constante de premiers jumeaux

\Pi _{2}=\prod _{p>2}\left(1-{\frac {1}{(p-1)^{2}}}\right)=0.6601618...

Ici le produit concerne les nombres premiers supérieur à 2.

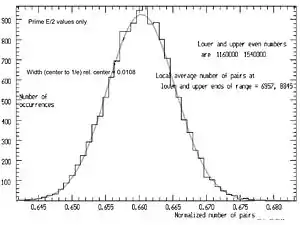
Le pic formé en sélectionnant uniquement les valeurs de $E/2$ qui sont premiers est d'un intérêt particulier. Le facteur de produit dans l'équation (1) est alors très proche de 1. Le pic est très proche d'une forme Gaussienne (en gris). Pour cette gamme de valeurs de E, l'emplacement du sommet est à 0,03 % de l'idéal $\Pi _{2}$ .

Quand les histogrammes sont formés pour les moyennes de différentes valeurs de E, la largeur de ce (premier uniquement) pic se trouve être proportionnelle à $1/{\sqrt {g_{pav}(E)}}$ .

Articles connexes

Conjecture de Goldbach

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Goldbach's comet » (voir la liste des auteurs).

Fliegel, Henry F.; Robertson, Douglas S.; "Goldbach's Comet: the numbers related to Goldbach's Conjecture”; Journal of Recreational Mathematics, v21(1) 1-7, 1989.
G. H. Hardy and J. E. Littlewood, "Some problems of 'partitio numerorum'; III: on the expression of a number as a sum of primes", Acta Mathematica, vol. 44, pp. 1-70, 1922.

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Fliegel, Henry F.; Robertson, Douglas S.; "Goldbach's Comet: the numbers related to Goldbach's Conjecture”; Journal of Recreational Mathematics, v21(1) 1-7, 1989.

[2] G. H. Hardy and J. E. Littlewood, "Some problems of 'partitio numerorum'; III: on the expression of a number as a sum of primes", Acta Mathematica, vol. 44, pp. 1-70, 1922.