Concentration de contrainte
La concentration de contrainte est un phénomène survenant lorsque la section d'une pièce varie de manière brutale : trou (perçage), rainure, épaulement, gorge, fond de fissure, etc.

Constatation
Une pièce présente des points de fragilité dus à la forme. On constate que l'apparition des fissures, et la rupture, a en général lieu dans des zones présentant des angles vifs rentrants ou bien des perçages. Par exemple :
- sur un mur, les fissures partent souvent des angles des portes ou des fenêtres ;
- pour faire du papier prédécoupé (timbres non-autocollants, carnets à souche, chèques, coupons de réduction, vignette de référence d'un courrier, vignette d'assurance automobile en France, …), on pratique de petits trous sur la périphérie de la zone à découper.
- Il est plus facile de casser proprement un morceau de chocolat en mettant l'entaille séparant les carreaux en traction qu'en compression.
Calcul de la contrainte maximale dans une structure de type poutre
Dans la théorie des poutres, on suppose que la section droite varie « lentement ». On peut alors déterminer les contraintes nominales :
- traction : ;
- torsion d'une pièce circulaire : , ;
- flexion autour de l'axe z : , .
où N est l'effort normal, S est l'aire de la section droite, les M sont des moments de flexion/torsion, les I sont des moments quadratiques axiale/polaire (ou « inerties ») et V est la distance à la fibre la plus éloignée.
Lorsque la section droite varie brutalement, ce calcul n'est plus valable. C'est le cas notamment lorsqu'il y a un épaulement, un congé, un perçage. On constate que les contraintes locales sont bien plus élevées que la contrainte nominale.
Dans la pratique, pour déterminer de manière simple (« à la main ») les contraintes maximales :
- on détermine les contraintes nominales σ0 et τ0, qui sont les contraintes calculées de manière classique sur la section la plus petite ;
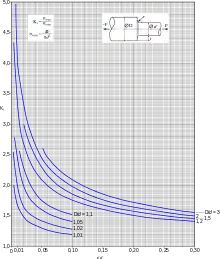
- on détermine un coefficient de concentration de contraintes, Kt, à l'aide d'un abaque, selon la géométrie de la pièce et la nature de la sollicitation ;
les contraintes maximales valent alors :
- σmax = Kt1×σ0
- τmax = Kt2×τ0
(le Kt n'a aucune raison d'être le même pour la contrainte normale et la cission). On peut aussi remplacer ce calcul manuel par une mesure ou un calcul par éléments finis.
Calcul de la contrainte maximale dans une structure de type plaque
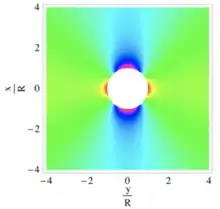
Dans une plaque (structure plane dont l'épaisseur est faible devant les autres dimensions), si les dimensions de la rainure ou du perçage sont faibles devant la largeur et la longueur de la plaque ("plaque infinie"), il existe des solutions analytiques[1], basées sur la mécanique des milieux continus permettant de calculer les coefficients de concentration de contraintes Kt aux abords du défaut. Notamment pour une plaque infinie percée d'un trou parfaitement cylindrique mise en traction[1]:
La solution analytique de la contrainte orthoradiale pour cette situation est représentée sur la Figure ci-contre.
Pour une plaque infinie percée d'un défaut elliptique mise en traction, de rayon dans la direction orthogonale à l'axe de traction et dans la direction de l'axe de traction[1]:
On remarque avec cette équation que plus le défaut est aplati ( plus petit que ) plus la concentration de contrainte est grande. Cela paraît contre-intuitif, mais dans une grande structure (face aux dimensions du défaut), il faut mieux avoir un gros défaut rond ( = ) que petit mais aplati ( << ).
Cette dernière expression de concentration de contrainte, quand < peut se ré-écrire en termes de demi-longueur de défaut () et de rayon de courbure de fond de défaut (). On a alors en traction:
Soulignant qu'il faut éviter un faible rayon de courbure. Dans le cas d'une plaque non-infinie, cette dernière expression peut s'adapter avec un facteur correctif[2] pour obtenir une valeur approchée:
la section de la plaque (plan orthogonal à l'axe de traction) loin du défaut, la section minimale, soit cette même section à laquelle on retire la surface projetée du défaut (2 fois l'épaisseur). Cette solution peut être généralisée à d'autres formes ou positions (par exemple débouchant à la surface) de défauts et pour la torsion[2].
Cas des assemblages collés
Selon la théorie de Volkersen, il y a une concentration de contrainte aux bords des joints de colles qui augmente avec la longueur du joint. Cette augmentation limite la force transmissible par unité de largeur du joint collé[3].
Notes et références
- « Concentration de contrainte dans une plaque trouée en traction, correction de travaux pratiques, École des Mines de Paris », sur http://mms2.ensmp.fr,
- Michael Ashby, Hugh Shercliff, David Cebon, Matériaux, Ingénierie, science, procédé et conception, PPUR, (lire en ligne), page 23
- Volkersen, O., Recherche sur la théorie des assemblages collés, Construction métallique, no 4, pp. 3-13, 1965.
Voir aussi
Bibliographie
- (en) E. F. Bruhn, Analysis and Design of Flight Vehicle Structures, Jacobs Publishing Inc., (ISBN 978-0-9615234-0-4)
- Jean-Louis Fanchon, Guide de mécanique : Sciences et technologies industrielles, Nathan, , 543 p. (ISBN 978-2-09-178965-1), p. 284-286, 312-313, 339-340
- (en) Walter D. Pilkey, Peterson's stress concentration factor, 2, , 544 p. (ISBN 978-0-471-53849-3)
- Portail des sciences des matériaux