Constante de Legendre

La constante de Legendre est une constante mathématique proposée par le mathématicien Adrien-Marie Legendre et qui n'a aujourd'hui plus qu'un intérêt historique.

En rouge, les 100 000 premiers termes de la suite ${\displaystyle a_{n}=\ln(n)-{\frac {n}{\pi (n)}}}$.

Pour les articles homonymes, voir Legendre.

Legendre conjecture en 1808 une forme précise de ce qu’on appellera plus tard le théorème des nombres premiers. Il écrit : « Quoique la suite des nombres premiers soit extrêmement irrégulière, on peut cependant trouver avec une précision très satisfaisante, combien il y a de ces nombres depuis 1 jusqu’à une limite donnée x. La formule qui résout cette question est

${\displaystyle y={\frac {x}{\log .x-1.08366}}}$

log.x étant un logarithme hyperbolique[1]. » En d’autres termes, Legendre affirme que

${\displaystyle \pi (x)={\frac {x}{\log(x)-A(x)}}}$

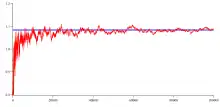
où ${\displaystyle \lim _{x\to \infty }A(x)=1{,}08366,}$ et où π(x) désigne la fonction de compte des nombres premiers inférieurs à x.

Le nombre ${\displaystyle A:=\lim _{x\to \infty }A(x)}$, qui existe, est appelé constante de Legendre. Mais sa valeur n’est pas celle supposée par Legendre.

En 1849, Tchebycheff[2] démontre que si la limite existe, elle doit être égale à 1. Une preuve plus simple est donnée par Pintz en 1980[3].

C'est une conséquence immédiate du théorème des nombres premiers (qui avait été démontré en 1896 indépendamment par Jacques Hadamard[4] et par Charles-Jean de La Vallée Poussin[5]), sous la forme plus précise démontrée en 1899 par La Vallée Poussin[6]

${\displaystyle \pi (x)={\rm {Li}}(x)+O\left(x\mathrm {e} ^{-a{\sqrt {\log x}}}\right)\quad {\text{lorsque }}x\to \infty ,}$

que

${\displaystyle \pi (x)={\frac {x}{\log x}}+{\frac {x}{(\log x)^{2}}}+o\left({\frac {x}{(\log x)^{2}}}\right),}$

et donc que A existe et vaut 1.