Constante parabolique universelle

La constante parabolique universelle est une constante mathématique.

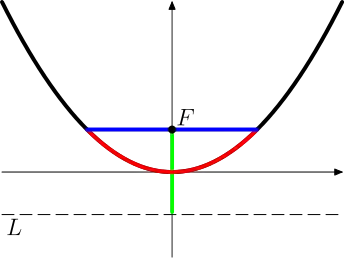
La constante parabolique universelle est la longueur rouge divisée par la longueur verte.

Elle est définie comme le rapport, noté P, pour toute parabole, de la longueur d'arc de la parabole formé par le latus rectum par le paramètre focal. Le paramètre focal est le double de la longueur focale[1]^,[2] (le foyer de la parabole est le point F et la droite directrice est notée L).

La valeur de P est

P=\ln(1+{\sqrt {2}})+{\sqrt {2}}=2.29558714939\dots

(suite A103710 de l'OEIS). Le cercle et la parabole sont uniques parmi les coniques à admettre un rapport universel. Le rapport analogue pour les ellipses et les hyperboles dépend de leur excentricités.

Démonstration

Soit ${\textstyle y={\frac {x^{2}}{4f}}}$ l'équation de la parabole. Le paramètre focal est $p=2f$ et le semilatus rectum vaut $\ell =2f$ .

{\begin{aligned}P&:={\frac {1}{p}}\int _{-\ell }^{\ell }{\sqrt {1+\left(y'(x)\right)^{2}}}\,dx\\&={\frac {1}{2f}}\int _{-2f}^{2f}{\sqrt {1+{\frac {x^{2}}{4f^{2}}}}}\,dx\\&=\int _{-1}^{1}{\sqrt {1+t^{2}}}\,dt&(x=2ft)\\&=\operatorname {arsinh} (1)+{\sqrt {2}}\\&=\ln(1+{\sqrt {2}})+{\sqrt {2}}.\end{aligned}}

Propriétés

P est un nombre transcendent.

Preuve. Supposons que P est algébrique. Alors

\!\ P-{\sqrt {2}}=\ln(1+{\sqrt {2}})

doit être algébrique. Cependant, par le théorème de Lindemann–Weierstrass,

\!\ e^{\ln(1+{\sqrt {2}})}=1+{\sqrt {2}}

serait transcendant, ce qui est faux. Donc P est transcendant.

On en déduit que P est irrationnel.

Autre apparition

La distance moyenne d'un point choisi au hasard dans le carré unitaire à son centre est

d_{\text{avg}}={P \over 6}.

Preuve.

{\begin{aligned}d_{\text{avg}}&:=8\int _{0}^{1 \over 2}\int _{0}^{x}{\sqrt {x^{2}+y^{2}}}\,dy\,dx\\&=8\int _{0}^{1 \over 2}{1 \over 2}x^{2}(\ln(1+{\sqrt {2}})+{\sqrt {2}})\,dx\\&=4P\int _{0}^{1 \over 2}x^{2}\,dx\\&={P \over 6}.\end{aligned}}

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Universal parabolic constant » (voir la liste des auteurs).

(en) Eric W. Weisstein, « {{{titre}}} », sur MathWorld(en) Eric W. Weisstein, « {{{titre}}} », sur MathWorld, a Wolfram Web resource.
Reese, « Pohle Colloquium Video Lecture: The universal parabolic constant » (consulté le 2 février 2005)

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Eric W. Weisstein, « {{{titre}}} », sur MathWorld(en) Eric W. Weisstein, « {{{titre}}} », sur MathWorld, a Wolfram Web resource.

[2] Reese, « Pohle Colloquium Video Lecture: The universal parabolic constant » (consulté le 2 février 2005)