Construction de Glushkov

La construction détermine, pour une expression rationnelle ${\displaystyle e}$ donnée, un automate non déterministe qui reconnaît le langage ${\displaystyle L(e)}$ dénoté par l'expression[4]. La construction est en quatre phases :

1.- Linéarisation de l'expression. Les symboles de l'alphabet figurant dans l'expression sont renommés de sorte que chaque symbole n'y figure qu'une fois. Notons ${\displaystyle A}$ l'ancien alphabet et ${\displaystyle B}$ le nouveau.

2a.- Calcul des ensembles ${\displaystyle P(e')}$, ${\displaystyle D(e')}$, et ${\displaystyle F(e')}$, où ${\displaystyle e'}$ est la version linéarisée de ${\displaystyle e}$. Le premier, ${\displaystyle P(e')}$ est l'ensemble des lettres qui peuvent commencer un mot du langage ${\displaystyle L(e')}$, et le second, ${\displaystyle D(e')}$, est celui des lettres qui peuvent finir un mot. Le dernier est l'ensemble des couples de lettres (facteurs de longueur 2) qui peuvent figurer dans les mots de ${\displaystyle L(e')}$. Ces ensembles se définissent par :

${\displaystyle P(e')=\{a\in B\mid aB^{*}\cap L(e')\neq \emptyset \}}$, ${\displaystyle D(e')=\{a\in B\mid B^{*}a\cap L(e')\neq \emptyset \}}$ et ${\displaystyle F(e')=\{u\in B^{2}\mid B^{*}uB^{*}\cap L(e')\neq \emptyset \}}$

Ils sont calculés par récurrence sur la structure de l'expression, comme expliqué plus bas, mais ils dépendent du langage et non de l’expression.

2b.- Calcul de l'ensemble ${\displaystyle \Lambda (e')}$ qui est composé du seul mot vide si le mot vide est dans ${\displaystyle L(e')}$, et est l'ensemble vide sinon, formellement

${\displaystyle \Lambda (e')=\{1\}\cap L(e')}$, où 1 est le mot vide.

3.- Calcul de l’automate du langage local défini par ${\displaystyle P(e')}$, ${\displaystyle D(e')}$, et ${\displaystyle F(e')}$ et ${\displaystyle \Lambda (e')}$. Par définition, le langage local défini par des ensembles ${\displaystyle P}$, ${\displaystyle D}$, et ${\displaystyle F}$ est l'ensemble des mots qui débutent par une des lettres de ${\displaystyle P}$, finissent par une des lettres de ${\displaystyle D}$, et dont tous les facteurs de longueur 2 sont dans ${\displaystyle F}$; en d'autres termes, c'est le langage :

${\displaystyle L=(PA^{*}\cap A^{*}D)\setminus A^{*}(A^{2}\setminus F)A^{*}}$,

augmenté éventuellement du mot vide.

Le calcul de l'automate pour le langage local dénoté par l'expression linéarisée est, à proprement parler, la construction de Glushkov. La construction de l'automate est possible grâce au construction classique : concaténation, union et itération d'automate.

4.- Effacement de la linéarisation, par identification des lettres qui avaient reçus des noms différents dans la première étape.

Automate par construction de Gluskkov — version linéaire.

Automate par construction de Gluskkov — version finale.

On considère[4] l'expression rationnelle

${\displaystyle e=(a(ab)^{*})^{*}+(ba)^{*}}$.

1.- La version linéarisée est

${\displaystyle e'=(a_{1}(a_{2}b_{3})^{*})^{*}+(b_{4}a_{5})^{*}}$.

On a distingué ici les lettres simplement en les indiçant par leur position dans l’expression.

2.- Les ensembles ${\displaystyle P}$, ${\displaystyle D}$, et ${\displaystyle F}$ des premières et dernières lettres, et des facteurs de longueur 2 pour l'expression linéarisée sont respectivement

${\displaystyle P(e')=\{a_{1},b_{4}\}}$, ${\displaystyle D(e')=\{a_{1},b_{3},a_{5}\}}$ et ${\displaystyle F(e')=\{a_{1}a_{2},a_{1}a_{1},a_{2}b_{3},b_{3}a_{1},b_{3}a_{2},b_{4}a_{5},a_{5}b_{4}\}}$.

Le mot vide est dans le langage, donc ${\displaystyle \Lambda (e')=\{1\}}$.

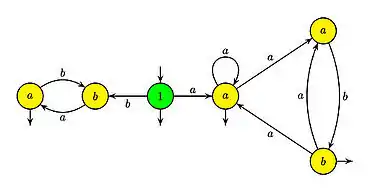
3.- L'automate du langage local

${\displaystyle L'=P'B^{*}\cap B^{*}D'\setminus B^{*}(B^{2}\setminus F')B^{*}}$

possède un état initial, noté 1, et un état pour chacune des cinq lettres de l'alphabet ${\displaystyle B=\{a_{1},a_{2},b_{3},b_{4},a_{5}\}}$. Il y a une transition de 1 vers les deux états dans ${\displaystyle P'}$, une transition de ${\displaystyle a}$ vers ${\displaystyle b}$ si ${\displaystyle ab}$ est dans ${\displaystyle F'}$, et les trois états de ${\displaystyle D'}$ sont terminaux ainsi que l'état 1. Toutes les transitions portent comme étiquette la lettre qui est l'état d'arrivée (et donc toutes les transitions arrivant en un état donnés ont la même étiquette, à savoir le nom de cet état).

4.- Obtention de l’automate pour ${\displaystyle L(e)}$ en supprimant les indices.

Le calcul des ensembles ${\displaystyle P}$, ${\displaystyle D}$, ${\displaystyle F}$ et ${\displaystyle \Lambda }$ se fait par récurrence sur la structure de l’expression. Il faut donc donner les valeurs pour 0, 1 (expressions de l'ensemble vide et du mot vide), des lettres, et le résultat des opérations ${\displaystyle +,\cdot ,*}$.

1.- Pour ${\displaystyle \Lambda }$, on a

${\displaystyle \Lambda (0)=\emptyset ,\Lambda (1)=\{1\}}$, et ${\displaystyle \Lambda (a)=\emptyset }$ pour toute lettre ${\displaystyle a}$,

puis

${\displaystyle \Lambda (e+f)=\Lambda (e)\cup \Lambda (f),\Lambda (e\cdot f)=\Lambda (e)\cdot \Lambda (f)}$ et enfin ${\displaystyle \Lambda (e^{*})=\{1\}}$

2.- Pour ${\displaystyle P}$, on a

${\displaystyle P(0)=P(1)=\emptyset }$ et ${\displaystyle P(a)=\{a\}}$ pour tout lettre ${\displaystyle a}$,

puis

${\displaystyle P(e+f)=P(e)\cup P(f),P(e\cdot f)=P(e)\cup \Lambda (e)P(f)}$ et enfin ${\displaystyle P(e^{*})=P(e)}$.

Les mêmes formules valent pour ${\displaystyle D}$, sauf pour le produit, où on a

${\displaystyle D(e\cdot f)=D(f)\cup D(e)\Lambda (f)}$.

3.- Pour les facteurs de longueur 2, on a

${\displaystyle F(0)=F(1)=F(a)=\emptyset }$ pour toute lettre ${\displaystyle a}$,

puis

${\displaystyle F(e+f)=F(e)+F(f),F(e\cdot f)=F(e)\cup F(f)\cup D(e)P(f)}$ et enfin ${\displaystyle F(e^{*})=F(e)\cup D(e)P(e)}$.

Les opérations coûteuses sont les produits d'ensembles pour le calcul de ${\displaystyle F}$.

On trouve souvent les notations First, Last, Follow ou Prem, Der, Suiv pour ${\displaystyle P}$, ${\displaystyle D}$, et ${\displaystyle F}$ respectivement.

L'automate obtenu est non déterministe, et de même taille (comptée en nombre d'états) que la taille (comptée en nombre de symboles) de l'expression rationnelle. Il a été observé[1] que l'automate de Glushkov est le même que l'automate obtenu en supprimant les ε-transitions de l'automate obtenu par la méthode de Thompson.

On note n le nombre de caractères présents dans l’expression rationnelle définissant le langage.

NB : on entend par caractère toute apparition d’une lettre ou d’un symbole + , . , * , ( , )

Exemple : ${\displaystyle e=(a(ab)^{*})^{*}+(ba)^{*}}$ contient 18 caractères.

1- Linéarisation de l’expression (passage de e à e’)

(Exemple : ${\displaystyle e=(a(ab)^{*})^{*}+(ba)^{*}}$ devient ${\displaystyle e'=(a_{1}(a_{2}b_{3})^{*})^{*}+(b_{4}a_{5})^{*})}$ Complexité : ${\displaystyle O(n)}$

2- Construction des ensembles définissant le langage local (P(e’), D(e’), et F(e’) déjà définis sur Wikipédia)

Peut se faire en un seul parcours, en effectuant un nombre fini de tests en fonction du symbole rencontré (ce sont bien sûr les symboles qui définissent)

Donc, on obtient une complexité en ${\displaystyle O(n)}$.

3- Construction de l’automate à l’aide des ensembles

Il s’agit d’un parcours de F(e’), commençant par un facteur dont la lettre de gauche est dans P(e’). Ensuite, on cherche un autre facteur commençant par la lettre qui termine le premier, et ainsi de suite...

(Exemple : Si on commence, par ${\displaystyle a_{1}}$, on lit d’abord ${\displaystyle a_{1}a_{2}}$, puis ${\displaystyle a_{2}b_{3}}$. Et comme ${\displaystyle b_{3}}$ est dans D(e’), on s’arrête)

En effet, le parcours s’arrête lorsqu’on aboutit à un état terminal (un élément de D(e’)).

Chaque chemin ainsi construit a donc une complexité en ${\displaystyle O(n)}$, mais comme il peut y avoir dans le pire des cas n chemins, on obtient une complexité en ${\displaystyle O(n^{2})}$.

4- Suppression des indices en ${\displaystyle O(n)}$.

Il est clair que les étapes 1 et 4 se font en temps fini.

2- Il y a un nombre fini de caractères dans une expression rationnelle, donc un nombre fini de facteurs de longueur 1 et 2. Donc les ensembles P(e’), D(e’), et F(e’) sont finis.

3- On a évoqué la répartition de la construction de l’automate en chemins. Il suffit alors de montrer qu’un chemin est fini pour conclure.

On choisit un élément de P(e’), et on construit un chemin comme expliqué précédemment.

Si l’une des lettres réapparaît dans le chemin, alors on a construit un cycle, donc on peut terminer le chemin maintenant, sans changer l’automate.

Sinon, alors on visite toutes les lettres de l’expression rationnelle, et comme elles sont en nombre fini, on arrive obligatoirement sur un élément de D(e’) en temps fini, donc le chemin est construit.

Donc l’algorithme termine. L’automate ainsi construit est non déterministe, et comporte autant d’états qu’il y a de lettres dans l’expression linéarisée e’.

Le calcul de l'automate à partir de l'expression intervient dans de nombreuses circonstances, et a été utilisé de manière systématique dans des fonctions de recherche de motifs dans les textes, comme la commande grep de Unix. Les spécifications des formats XML font appel aussi à ces constructions; pour les rendre efficaces, des expressions régulières d'un type particulier appelées expressions déterministes ont été étudiées[5]^,[1].

• (en) Gérard Berry et Ravi Sethi, « From regular expressions to deterministic automata », Theoretical Computer Science, vol. 48,‎ 1986, p. 117-126 (ISSN 0304-3975).
• (en) Victor M. Glushkov, « The abstract theory of automata », Russian Mathematical Surveys, vol. 16,‎ 1961, p. 1-53 (ISSN 0036-0279).
• (en) Jean Berstel et Jean-Éric Pin, « Local languages and the Berry-Sethi algorithm », Theoretical Computer Science, vol. 155,‎ 1996, p. 439–446.
• (en) Jean-Éric Pin, « Finite automata », dans Jean-Éric Pin (éditeur), Handbook of Automata Theory, 2010
• Olivier Carton, Langages formels, calculabilité et complexité, 2008 [détail de l’édition] (lire en ligne)
• Jacques Sakarovitch, Éléments de théorie des automates, Vuibert, 2003, 816 p. (ISBN 978-2-7117-4807-5) — Traduction anglaise avec corrections : Elements of Automata Theory, Cambridge University Press 2009 (ISBN 9780521844253).
• Djelloul Ziadi, Jean-Luc Ponty et Jean-Marc Champarnaud, « Passage d’une expression rationnelle à un automate fini non déterministe », Bulletin of the Belgian Mathematical Society Simon Stevin, vol. 4, n^o 1,‎ 1997, p. 177–203 (lire en ligne [PDF])

• Portail de l'informatique théorique