Constructions du milieu d'un segment

Construction à la règle et au compas d'une médiatrice et du milieu d'un segment

La méthode dans ce cas est de construire au compas la médiatrice du segment, le milieu étant l'intersection du segment avec sa médiatrice.

Tout point constructible à la règle et au compas est aussi constructible au compas seul[1]. Le milieu d'un segment peut donc être construit au compas seul.

Le principe consiste à utiliser les propriétés de la figure ci-dessous dans laquelle le segment [AB] a pour longueur 1, les segments [AC] et [CD] ont pour longueur 2 et les segments [AD] et [DI] ont pour longueur 1. Les triangles ACD et ADI sont semblables car ils sont tous les deux isocèles et partagent un même sommet de base. Le segment [AI] a donc pour longueur 1/2 et le point I est le milieu du segment [AB]. Il s'agit maintenant de reproduire les points de la figure uniquement au compas.

On construit d'abord le point C, symétrique de A par rapport à B[2]. Le point D et son symétrique D' sont situés sur le cercle de centre C et de rayon CA et sur le cercle de centre A et de rayon AB. Le point I est situé sur les cercles de centre D et D' et de rayon DA = D'A.

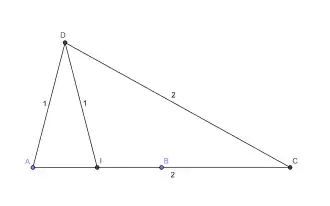Construction du milieu de [AB] au compas seul. Figure de base

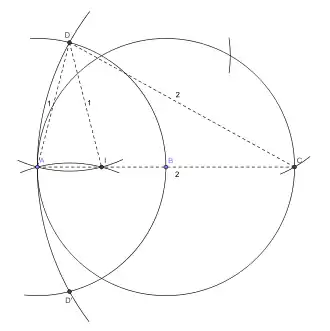Construction du milieu de [AB] au compas seul. Réalisation

Cette construction est la cinquième proposée par Lorenzo Mascheroni pour déterminer le milieu d'un segment. Il la présente comme la construction la plus simple mais fait remarquer que sa réalisation pratique est imprécise car les arcs de cercle se coupent suivant un angle trop aigu[3]. Ses autres constructions utilisent le même principe mais construisent des parallélogrammes moins étroits comme le parallélogramme AIDE où E est le symétrique de D' par rapport à A.

Construction d'un parallélgoramme de diagonale [AB]

Le té-virtuel est un instrument de dessin qui permet de tracer une parallèle à une droite quelconque passant par un point quelconque. En pratique on peut utiliser un té, ou plus simplement une équerre coulissant le long d'une règle.

Nous n'avons pas besoin de situer la figure dans un plan métrique, il suffit de travailler dans un espace affine. Un tel type de plan ignore les distances, les cercles et les angles droits, il ne connaît que le parallélisme. Un tel type de plan ignore encore les vecteurs, a fortiori les barycentres et encore plus l'isobarycentre. Il ignore les carrés, les rectangles, les losanges, il ne connaît que les parallélogrammes. Et dans un parallélogramme les diagonales se coupent en un point que l'on appelle "milieu", plus exactement "milieu-affine".

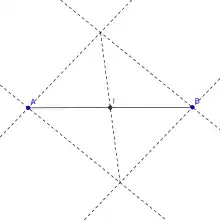
La méthode consiste à

• tracer à partir de A deux droites quelconques d1 et d2
• à l'aide de l'instrument traceur de parallèles, tracer en B une parallèle à d1 et une parallèle à d2
• on obtient ainsi un parallélogramme ACBD
• le milieu I cherché est l'intersection des deux diagonales du parallélogramme.

Il n'est pas possible, à la règle seule de construire une parallèle à une droite donnée ou le milieu d'un segment donné[4]. En revanche une telle construction est possible si l'on dispose de deux couples de droites parallèles[5].

Principe de base

Trapèze avec ses deux centres d'homothétie et les milieux de ses bases.

La construction s'appuie sur les deux remarques suivantes : Soient A et B deux points distincts,

• si on connait une droite parallèle à la droite (AB), il est possible à la règle seule de déterminer le milieu du segment [AB]
• si on connait le milieu du segment [AB], pour tout point M, il est possible de construire à la règle seule la parallèle à (AB) passant par M

Ces deux observations s'appuient sur les propriétés du trapèze et les deux homothéties qui lui sont associées.

On considère un trapèze ABCD avec (AB) et (CD) parallèles, AB différent de CD et on note O le point d'intersection des droites (BC) et (AD), et O' celui des droites (BD) et (AC).

L'homothétie de centre O qui transforme A en D transforme la droite (AB) en la droite (DC), donc transforme le point B en C. Cette même homothétie transforme le milieu I de [AB] en le milieu E de [CD]. Les points OIE sont donc alignés. On démontre de même que les points O'IE sont alignés. Le point I est donc situé sur la droite (OO').

On observe aussi que le point C est situé sur la droite (OB) et la droite (O'A).

Construction du milieu de [AB] connaissant une droite strictement parallèle à (AB)

on choisit un point O situé de l'autre côté de (d) par rapport à A et B. Les droites (OA) et (OB) coupent (d) en D et C construisant ainsi un trapèze. On construit alors le point O' point d'intersection des diagonales (AC) et (BD). Le milieu I du segment [AB] est le point d'intersection de la droite (OO') avec (AB).

Construction (étape 1)

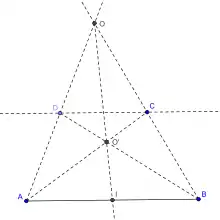Construction (étape 2)

Construction d'une parallèle à (AB) passant par M connaissant le milieu I de [AB]

on choisit un point O situé sur (AM) de l'autre côté de M par rapport à A. Les droites (OI) et (MB) se rencontrent en O'. Les droites (AO') et (BO) se rencontrent en C. Les droites (MC) et (AB) sont alors parallèles.

Construction (étape 1)

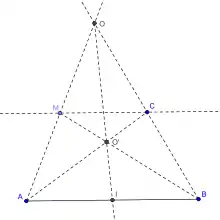Construction (étape 2)

Utilisation des couples de droites parallèles

On suppose donnés deux couples de droites parallèles dessinant un parallélogramme ABCD. L'existence d'une droite parallèle à (AB) permet de construire le milieu de [AB]. De même, on peut construire les milieux de [BC], [CD], [DA].

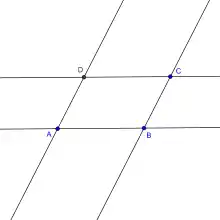Couples de départ

Un milieu

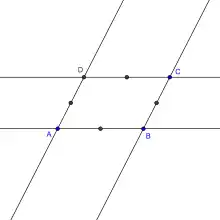Quatre milieux

En joignant les milieux des côtés opposés, on complète la figure de base en deux triplets de droites parallèles. Une droite (d) et un point M étant donnés, il est alors possible, en utilisant l'un ou l'autre des triplets de découper sur (d) un segment et son milieu. Il est alors possible de tracer par le point M, une parallèle à la droite (d). Un segment [PQ] étant donné, il est alors possible de construire une parallèle à (PQ) passant par un point M quelconque, puis, comme on connait une droite parallèle à la droite (PQ), il est possible, à la règle seule, de construire le milieu de [PQ]

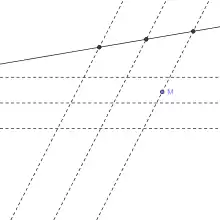Triplets de droites parallèles

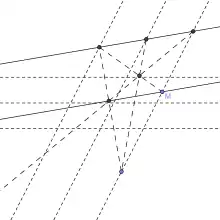Construction d'une parallèle

Construction d'un milieu

Le théorème de Poncelet-Steiner permet d'affirmer que tout point constructible à la règle et au compas peut être construit à la règle seule à condition que soit donné au départ un seul cercle et son centre. Le milieu I étant constructible à la règle et au compas il est aussi constructible à la règle et au cercle.

La méthode suivante s'appuie sur le fait que l'on peut construire simplement à la règle seule une parallèle à une droite (d) passant par un point M pour peu que la droite coupe le cercle[6]. On utilise pour ce faire le fait qu'une corde [PQ] du cercle distincte d'un diamètre possède une parallèle naturelle passant par les points P' et Q' diamétralement opposés à P et Q sur le cercle. On peut tout aussi simplement construire le milieu du segment [AB] si la droite (AB) coupe le cercle selon une corde distincte d'un diamètre : la droite (AB) coupant le cercle suivant la corde [PQ], on peut alors construire la droite [P'Q'] parallèle à (AB) et l'on sait (voir Construction du milieu de [AB] connaissant une droite strictement parallèle à (AB) ) déterminer à la règle seule le milieu d'un segment si on connait une droite parallèle à ce segment.

Enfin, si la droite (AB) ne coupe pas le cercle, on peut choisir un point C sur le cercle tel que les droites (AC) et (BC) ne soient ni des tangentes au cercle ni des diamètres du cercle. Il est alors possible de construire les milieux de [AC] et [BC]. Comme les trois médianes du triangle ABC sont concourantes, on peut alors construire le milieu de [AB]

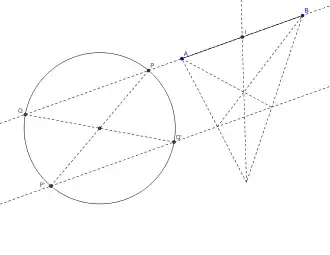Construction du milieu de [AB] quand (AB) coupe le cercle

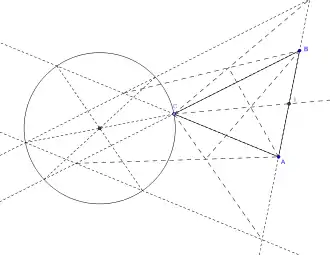Construction du milieu de [AB] à l'aide du triangle ABC

• Construction à la règle seule

• Portail de la géométrie