Contractions hiérarchiques
En mathématiques appliquées, la méthode des contractions hiérarchiques est une technique destinée à réduire le temps de calcul du plus court chemin grâce à la construction d'une représentation dite "contractée" du graphe initial sur laquelle sont exécutés des algorithmes adaptés aux recherches sur structure multi-niveaux. Les temps de calcul d’itinéraire issus de cette méthode peuvent être drastiquement plus rapides que l'algorithme de Dijkstra et surpasser de plus anciennes méthodes d'optimisation telles que les Highway Hierarchies. Elle a été proposée en 2008 par Robert Geisberger, Peter Sanders, Dominik Schultes, et Daniel Delling de l’université Karlsruhe Institute of Technology d’Allemagne[1],[2]. Comme Dijkstra, cette méthode peut permettre au sein d’un graphe routier, la récupération d’un plus court chemin comme la récupération de zones de chalandise.
Cette méthode peut se scinder en au moins 2 phases :
- Une phase de prétraitement du graphe initial.
- Une phase d'exécution de la requête sur la représentation contractée du graphe.
La première phase est vouée à générer plusieurs couches successives de représentation du graphe initial de plus en plus synthétiques.[3],[4]
Aujourd'hui plusieurs outils open-source de calcul d'itinéraire utilisent cette méthode : OSRM[5], OpenTripPlanner[6], Graphhopper[7], Tempus[8], RoutingKit[9]
Phase de contraction
La contraction d’un sommet d’un graphe consiste à le faire disparaitre de la couche de représentation supérieure tout en conservant l’information de distance entre les sommets restants. En phase de contraction, la sélection des sommets est le fruit de la conjonction de différents critères :
- nœuds dont la contraction engendrera une plus grande réduction du nombre d’arêtes pour la couche supérieure de représentation du graphe,
- nœuds dont la contraction sera la plus rapide,
- nœuds dont aucun voisin n'a encore été contracté,
- etc.
Graphe initial
Soit le graphe initial suivant :
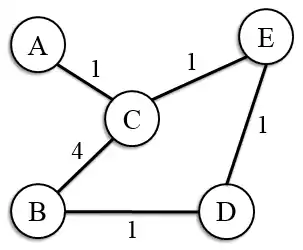 Graphe initial |
Désirant contracter arbitrairement le nœud C, A-C-E et A-C-B étant des plus courts chemins, à la couche précédente de représentation du graphe, 2 raccourcis doivent être insérés : AB et AE. B-C-E n’étant pas un plus court chemin[11], il n’y a pas besoin d’insérer de plus court chemin entre B et E.
Nouvelle représentation du graphe
La nouvelle représentation du graphe à la suite de la contraction de C sera de la forme :
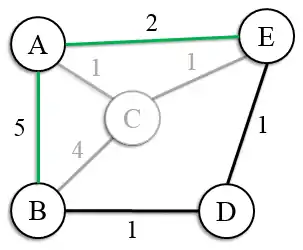 Graphe initial |
Algorithme de recherche
Pour un graphe non orienté, une fois la structure multi-niveaux construite, les algorithmes de recherche d’un plus court chemin n’ont plus qu’à réaliser des recherches de Dijkstra ascendantes à partir de la source et de la destination jusqu’à la découverte d’un nœud commun.
Exemple d’exécution de recherche de plus court chemin sur structure multi-niveaux entre u et y
Graphe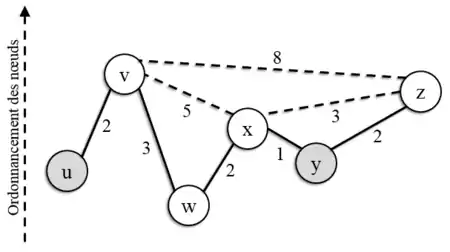 | Etape 1 : Lancement d’une recherche bidirectionnelle |
| Etape 2 : x est choisi comme second nœud à traiter pour la recherche partant de y 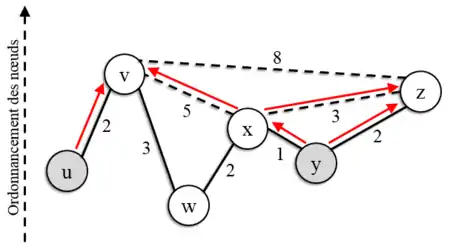 | Etape 3 : Plus court chemin trouvé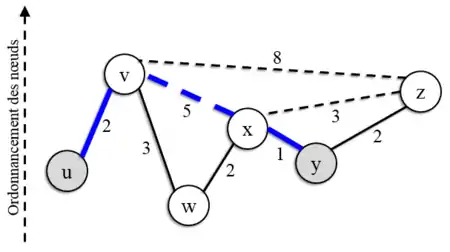 |
Etape 4 : Relaxation des raccourcis |
Une recherche de couverture à partir d’un sommet devra par contre suivre les embranchements ascendants et descendants jusqu’à répondre à la condition d’arrêt définie. Pour plus d’information sur le calcul d’isochrones sur structure multi-niveaux voir la thèse de Valentin Buchhold[12].
Pour un graphe orienté, il faudra construire 2 structures multi-niveaux soit une construite en considérant les sens des arcs du graphe d'origine et une construite en considérant une inversion du sens de ces arcs. Ensuite, pour obtenir un plus court chemin il suffira de lancer l'algorithme Dijkstra sous sa forme multi-niveaux partant de la source sur la structure obtenue à partir du graphe d'origine et à partir de la destination sur l'autre structure jusqu'à l'obtention d'un sommet commun.
Contractions Hiérarchiques Adaptables
Pour rendre ce type d’architecture plus réactif aux modifications régulières de pondérations de segments du graphe, une méthode nommée "Customizable Contraction Hierarchies" a été proposée[13]. Une telle méthode permet de répondre à des requêtes de recherche du plus court chemin sous quelques millisecondes pour des jeux de données de l’échelle d’un continent tout en gardant une flexibilité de pondération des segments routiers. Afin de faciliter la compréhension et la mise en œuvre de cette méthode, une bibliothèque C++ nommée RoutingKit[9] a été implémentée et diffusée sur GitHub par le groupe du professeur Dorothea Wagner du Karlsruhe Institute of Technology d’Allemagne.
Notes et références
- (en) R. Geisberger, P. Sanders, D. Schultes et D. Delling, Contraction Hierarchies: Faster and Simpler Hierarchical Routing in Road Networks - International Workshop on Experimental and Efficient Algorithms, Université Karlsruhe d'Allemagne, (lire en ligne), pages 319-333
- (en) R. Geisberger, Contraction Hierarchies: Faster and Simpler Hierarchical Routing in Road Networks, Université Karlsruhe d'Allemagne, (lire en ligne)
- Hannah Bast, « Efficient Route Planning, Lectures »,
- Ivan Škugor, « Contraction hierarchies », (consulté le )
- (en) « OSRM – Open Source Routing Machine »
- (en) « Wiki – OpenTripPlanner »
- (en) « Web – GraphHopper »
- (en) « GitHub – Tempus »
- (en) « GitHub – RoutingKit »
- (en) M. Tandy, « Contraction Hierarchies path finding algorithm, illustrated using three.js », Blog de Michael Tandy, (lire en ligne)
- La valeur totale de ce chemin est 4 + 1 = 5, supérieure à celle du chemin B-D-E, qui est le plus court chemin de B à E. La contraction portant sur le nœud C, le chemin B-C-E n'est pas retenu par le calcul de l'algorithme de contraction.
- (en) [3] Buchhold Valentin, Fast Computation of Isochrones in Road Networks, Université Karlsruhe d'Allemagne, (lire en ligne)
- (en) J. Dibbelt, B. Strasser, D. Wagner, « Customizable Contraction Hierarchies », International Symposium on Experimental Algorithms, (lire en ligne)