Courbe d'indifférence
En économie, une courbe d'indifférence est l'ensemble des combinaisons de deux biens qui procurent au consommateur un niveau de satisfaction identique[1].
Contexte et définitions
En microéconomie, une courbe d'indifférence est une courbe permettant de représenter l'ensemble des combinaisons de deux biens pour lesquels un agent économique (tel qu'un consommateur ou une entreprise) serait indifférent, c'est-à-dire qu'il n'aurait pas de préférence pour une combinaison plutôt qu'une autre en termes d'utilité ordinale. Les courbes d'indifférence servent à analyser le choix des agents économiques.
Par exemple, si un consommateur est satisfait de la même façon par 1 pomme et 4 bananes, 2 pommes et 2 bananes, ou 5 pommes et 1 banane, alors ces combinaisons seront reliées par la même courbe d'indifférence.
Pour un couple de biens donné, une infinité de courbes d'indifférence peut être dessinée. Il est fait l'hypothèse que le consommateur préfère les combinaisons de biens représentant un plus haut niveau de consommation (hypothèse de non satiété ou Postulat de non saturation). Le consommateur rationnel va choisir le panier de biens pour lequel il aura la courbe d'indifférence la plus élevée, étant donnés les choix qui s'offrent à lui. La pente d'une courbe d'indifférence en un point est donné par le Taux marginal de substitution.
Histoire et discussion
Le concept de courbe d'indifférence, imaginé initialement par Francis Edgeworth, a été développé par Vilfredo Pareto et d'autres dans la première partie du XXe siècle. Le recours à ce concept a permis à l'analyse économique d'utiliser le concept de préférences dans la détermination des choix plutôt que celui d'utilité cardinale. Néanmoins, Vito Volterra fit remarquer à Pareto que s’il y a plus de deux biens, il peut être impossible de remonter à la fonction d’utilité. On sait aujourd’hui que cette question d’intégrabilité implique un effet de substitution symétrique (voir Théorie du consommateur). Les Néoclassiques supposent que le consommateur est rationnel, il choisit le panier de biens qu'il préfère, parmi tous ceux qu'il peut acheter.
Selon Murray Rothbard, un économiste et philosophe libertarien, un des inconvénients de ce genre de représentation est d'habituer les économistes à raisonner comme si on pouvait connaître les jugements de valeur des gens sans qu'ils les expriment réellement par leurs actions concrètes, voire comme si on pouvait les mesurer. D'après lui, c'est à cause de ce genre d'irréalisme qu'on sous-estime le caractère arbitraire voire contradictoire des raisonnements sur les "effets externes" et les "services collectifs" - qu'on appelle aussi, de manière incorrecte, des "biens publics". Cette opinion est largement minoritaire parmi les économistes. En effet, en observant le consommateur lorsqu'il fait ses achats, il est possible de déduire ses préférences (voir théorie de la préférence révélée).
Caractéristiques
Propriétés des courbes d'indifférence
Les courbes d'indifférence ont traditionnellement les propriétés suivantes :
- les courbes d'indifférence ne se coupent pas. C'est la conséquence de l'hypothèse de transitivité des préférences.
- les courbes d'indifférence ne sont jamais croissantes, en raison de l'hypothèse de non saturation des préférences. D'où sa pente négative. La forme décroissante de cette courbe est la seule façon pour le consommateur de maintenir son utilité : il doit substituer un bien à un autre (si la fonction était croissante, cela voudrait dire que le consommateur pourrait augmenter sa consommation des deux biens tout en gardant la même utilité, ce qui contredit bien l'hypothèse de non satiété).
Complétude : les consommateurs connaissent leurs préférences individuelles. Ils peuvent choisir entre consommer le couple X ou le couple Y. Ils savent si X est préféré à Y, Y est préféré à X, ou s'ils sont indifférents entre consommer X ou Y.
Transitivité : si un consommateur préfère le couple X au couple Y, et préfère le couple Y au couple Z, alors il préférera le couple X au couple Z.
Continuité : cela signifie que vous pouvez choisir de consommer n'importe quelle quantité d'un bien. Par exemple, je peux boire 11 ml de soda, ou 12 ml, ou 132 ml. Je ne suis pas contraint de boire 2 litres ou rien. Voir fonction continue en mathématiques.
Non satiété (monotonie) : c'est l'idée qu'il n'y a jamais de saturation de la consommation d'un bien.
Convexité : le consommateur préfère un panier équilibré de biens plutôt qu'un seul bien.
Exemple de courbes d'indifférence

Le consommateur préfèrera être sur CI 3 que sur CI 2, et préfèrera CI 2 à CI 1, mais peu lui importe où il se trouve sur les courbes d'indifférence. La pente d'une courbe d'indifférence, appelée par les économistes le taux marginal de substitution (en un point, car ce taux varie dans ce cas sur la courbe), montre le taux pour lequel le consommateur voudra bien donner un peu d'un bien en échange de l'autre bien. La courbe est convexe car le taux marginal de substitution est décroissant. Pour la plupart des biens, le taux marginal de substitution n'est pas constant, ce qui donne une courbe d'indifférence strictement convexe.

Si les biens sont parfaitement substituables alors les courbes d'indifférences seront des droites parallèles. Le taux marginal de substitution est constant.
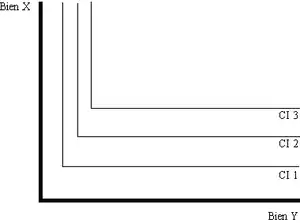
Si les biens sont parfaitement complémentaires alors les courbes d'indifférence seront en formes de L. Par exemple, si une recette de gâteau nécessite 3 cuillères de farine et 1 de sucre. Peu importe quelle quantité supplémentaire de farine vous utilisez, vous ne pourrez pas faire de gâteau supplémentaire sans sucre. Un autre exemple de complémentarité parfaite entre produits est la paire de chaussures. Le consommateur n'est pas plus satisfait d'avoir plusieurs chaussures du pied droit que s'il n'a qu'une chaussure du pied gauche. Les chaussures du pied droit supplémentaires ont une utilité marginale nulle sans la chaussure du pied gauche. Le taux marginal de substitution est soit zéro soit l'infini.
La théorie du consommateur utilise les courbes d'indifférence et la contrainte budgétaire pour élaborer les courbes de demande du consommateur.
Notes et références
- Pierre Cahuc et André Zylberberg, Le marché du travail, De Boeck Supérieur, (lire en ligne)