Courbe de Lebesgue
En mathématiques, et plus précisément en géométrie, la courbe de Lebesgue a été étudiée par le mathématicien français Henri Lebesgue en 1904. Elle consiste en une courbe continue, de l'intervalle [0, 1] dans le carré et qui remplit entièrement le carré. Elle constitue donc une courbe de remplissage.
Définition
Pour tout y élément de l'ensemble de Cantor, on a une décomposition en base 3 de la forme , où, pour tout k, est un chiffre valant 0 ou 2. On associe à ce réel y un point f(y) du plan de coordonnées . On définit ainsi une fonction f de l'ensemble de Cantor dans le carré . On prolonge ensuite f à l'intervalle [0, 1] tout entier de façon que, sur chaque intervalle composante connexe du complémentaire dans [0, 1] de l'ensemble de Cantor, le prolongement soit une fonction affine. Le prolongement obtenu est alors une fonction continue et surjective[1] de [0, 1] sur . Elle est en outre presque partout dérivable.
La courbe de Lebesgue peut aussi être réalisée en trois dimensions. Il suffit pour cela de scinder les chiffres de y en trois sous-familles.
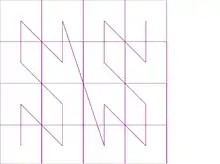
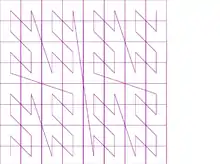
Calcul approché
Si on se limite à un calcul numérique limité à n chiffres , l'approximation de la courbe de Lebesgue que l'on obtient peut se représenter dans un quadrillage de 4n carrés, chacun possédant un côté de même longueur 1⁄2n. La courbe approximée passe par les centres de tous les carrés. En passant à la limite, on obtient la courbe de Lebesgue.
La construction de la courbe approchée peut se faire récursivement comme suit :
- A l'étape 0, la courbe C(0) se limite à un seul point, disposé au centre d'un carré. Ce point est à la fois point initial et point final de C(0).
- Pour n strictement positif, on divise un carré en quatre sous-carrés qu'on numérote de 0 à 3 selon le schéma ci-dessous :
| 1 | 3 |
| 0 | 2 |
On dispose dans chaque carré un exemplaire de la courbe C(n-1) calculée au rang précédent, puis, pour i variant de 0 à 2, on relie par un segment le point final de la courbe C(n-1) disposé dans le carré i au point initial de la courbe C(n-1) disposé dans le carré i+1. Le point initial de la courbe C(n) ainsi obtenue est le point initial de la courbe C(n-1) du carré 0, et le point final de la courbe C(n) est le point final de la courbe C(n-1) du carré 3.
Variantes
Il existe des variantes à la courbe de Lebesgue, notamment la courbe de Hilbert qui, elle, est une courbe à paramétrisation continue, contrairement à la courbe de Lebesgue qui supprime certaines discontinuités et les remplace par des fonctions affines.
Lien externe
Notes et références
- (en) James Dugundji, Topology, Dubuque (Iowa), Wm. C. Brown Publisher, , 447 p. (ISBN 0-697-06889-7), p. 105
- Portail de la géométrie