Courbe de la crêpe
En mathématiques, la courbe de la crêpe est une courbe en trois dimensions étudiée par William Kingdon Clifford. Son nom vient de la forme d'une crêpe lancée avec une poêle.
Équations
Une paramétrisation cartésienne possible est :
C'est donc une courbe biquadratique rationnelle.
Définitions
La courbe de la crêpe possède trois définitions : elle est l'intersection d'un cylindre de révolution avec
- un paraboloïde hyperbolique de même axe que le cylindre
- un conoïde de Plücker de même axe
- un cylindre parabolique de droite sommitale perpendiculaire à l'axe du cylindre .
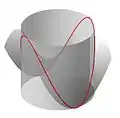 avec le paraboloïde hyperbolique
avec le paraboloïde hyperbolique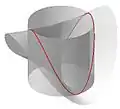 avec le conoïde de Plücker
avec le conoïde de Plücker avec le cylindre parabolique
avec le cylindre parabolique
Propriétés
- La courbe de la crêpe est une couronne sinusoïdale.
- La projection de la courbe sur un plan orthogonal à l'axe du cylindre donne un cercle ; les projections sur les plans d'équations et donnent des lemniscates de Gerono isométriques ; les projections sur les plans d'équations et donnent des portions de parabole.
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.