Courbe quintique
En mathématiques une courbe quintique est une courbe algébrique plane de degré 5. Elle peut être définie par un polynôme de la forme :
dont les coefficients sont dans un corps commutatif donné. L'équation a 21 coefficients, mais la courbe ne change pas si on les multiplie tous par une constante non nulle. On peut donc fixer U à 1 et se contenter de 20 coefficients. Il y a donc une infinité de quintiques, et chacune d'elles est identifiée par son passage par 20 points génériques.
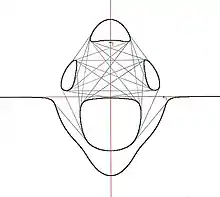
Caractéristiques
Une courbe quintique (n = 5) définie sur le corps des réels et irréductible peut avoir au maximum :
- (n – 1)(n – 2)/2 + 1 = 7 composantes connexes, d'après le théorème de Harnack[1].
Par ailleurs, les formules de Plücker montrent qu'elle peut avoir au plus :
- (n – 1)(n – 2)/2 = 6 points doubles ;
- n(n – 2)(n – 3)(n + 3)/2 = 120 bitangentes, c'est-à-dire de droites qui sont des tangentes à la courbe en 2 points ;
- 3n(n – 2) = 45 points d'inflexion.
Applications
Les courbes quintiques apparaissent dans l'étude des problèmes de courbes à réaction constante : quelle doit-être la forme de la courbe suivie par un point dans un champ de gravitation de sorte que la réaction du point sur la courbe soit constante ?
Exemples de courbes quintiques définies sur le corps des réels
- Courbe de Burnside
- Courbe kératoïde
- Courbe en étrier (it)
- Courbe en quilles
- Courbe de l'Hospital[2]
- Courbe de Mutasci
- Courbe sinusoïdale
- Maracas de Chioppa
- Butterfly Catastrophe
- Courbe à bulbe
- Feuille de Patarino
- Courbe en tulipe
- Courbe en gouttes
- Impulsion unique
- Double impulsion
- Courbe à point triple
- Courbe à trois nœuds coulants
- Courbe avec deux points de rebroussement et deux nœuds
- Courbe à 36 bitangentes
- Courbe avec 10 flexions
- Courbe à six composantes connexes
- Courbe à six nœuds
Illustrations
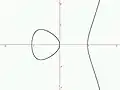 Courbe de Burnside
Courbe de Burnside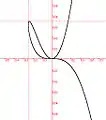 Courbe kératoïde
Courbe kératoïde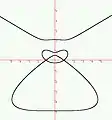
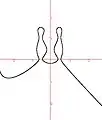 Courbe en quilles
Courbe en quilles Courbe de l'Hospital
Courbe de l'Hospital Courbe de Mutasci
Courbe de Mutasci Courbe sinusoïdale
Courbe sinusoïdale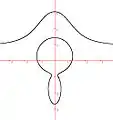 Maracas de Chioppa
Maracas de Chioppa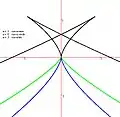 Butterfly Catastrophe
Butterfly Catastrophe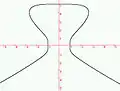 Courbe à bulbe
Courbe à bulbe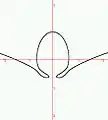 Feuille de Patarino
Feuille de Patarino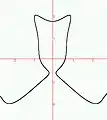 Courbe en tulipe
Courbe en tulipe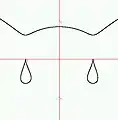 Courbe en gouttes
Courbe en gouttes Courbe à point triple
Courbe à point triple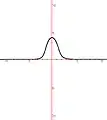 Impulsion unique
Impulsion unique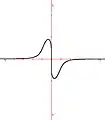 Double impulsion
Double impulsion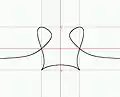 Courbe avec deux points de rebroussement et deux nœuds
Courbe avec deux points de rebroussement et deux nœuds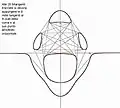 Courbe à 36 bitangentes
Courbe à 36 bitangentes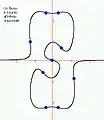 Courbe avec 10 flexions
Courbe avec 10 flexions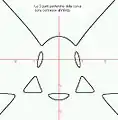 Courbe à six composantes connexes
Courbe à six composantes connexes Courbe à six nœuds
Courbe à six nœuds
Notes et références
- « Topologie des courbes algébriques planes réelles » (consulté le ).
- « Courbe à réaction constante, quintique de l'Hospital », sur mathcurve.
Voir aussi
Articles connexes
Liens externes
- « Quintique », sur mathcurve.com (site de courbes et surfaces maintenu par Robert Ferreol)
- (en) Eric W. Weisstein, « Quintic Curve », sur MathWorld (brève définition des courbes quintiques)
- (it) « Grafico quintica », sur ascifoni.com (exécutable pour tracer des courbes quintiques)
- Portail de la géométrie