Cubique de Tschirnhausen
En géométrie, la cubique de Tschirnhausen est une courbe algébrique définie par l'équation polaire
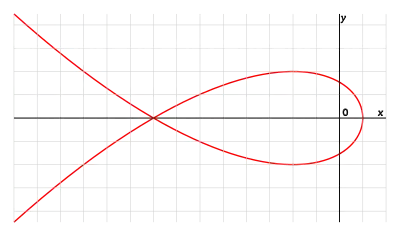
Histoire
Cette courbe fut étudiée par Ehrenfried Walther von Tschirnhaus, Guillaume de l'Hôpital et Eugène Catalan. Le nom de « cubique de Tschirnhausen » fut mentionné pour la première fois en 1900 par Raymond Clare Archibald, bien qu'elle soit parfois connue sous le nom de « cubique de L'Hôpital » ou « trisectrice de Catalan ».
Autres équations
Posons t = tan(θ/3). Selon la formule de De Moivre, cela donne :
ce qui donne une équation paramétrique. Le paramètre t peut être facilement éliminé, ce qui donne l'équation cartésienne
- .
Si la courbe est translatée horizontalement de 8a, les équations deviennent
ou
- ,
ce qui donne la forme polaire
- .
Propriétés
Caustique
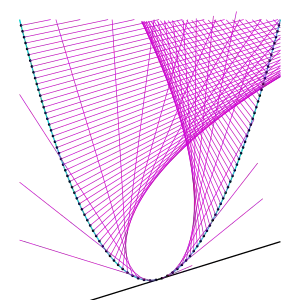
Les caustiques de parabole, lorsque la source lumineuse est à l'infini, sont des cubiques de Tschirnhausen. Elle est réduite à un point, le foyer de la parabole, lorsque la direction de la source est l'axe de la parabole.