Déferlement des vagues
Le déferlement des vagues est la déformation rapide du profil de l'onde, associé à la production de turbulence. L'onde qui déferle perd ainsi son énergie. On parle ainsi de déferlement pour des ondes de gravité de surface, comme les vagues, mais aussi pour les ondes internes. Dans les deux cas, outre la production d'énergie turbulente, le déferlement aboutit aussi à un transfert de quantité de mouvement : c'est le déferlement des vagues qui est la cause principale de l'accélération des courants de surface que l'on associe au vent (le vent génère les vagues qui génèrent le courant), ainsi que le courant de dérive littorale. C'est aussi le déferlement des ondes internes dans l'atmosphère qui participe au ralentissement des vents dans les régions montagneuses.

Dans le cas des vagues de longueur d'onde supérieure à un mètre, ce déferlement est généralement associé à une instabilité hydrodynamique de la crête de la vague, qui conduit à l'entrainement d'air sous la surface et la formation d'écume, ainsi que d'aérosols marins.
Pour les vagues les plus courtes, leur énergie est insuffisante pour former des bulles d'air, et le déferlement se manifeste par un bourrelet turbulent. Ce phénomène est par contre très visible sur des images infra-rouges, car le déferlement mélange la fine pellicule d'eau (généralement plus froide) de la surface avec l'eau de sub-surface.

Principe du déferlement
Le principe du déferlement des vagues est très simple : la vitesse de propagation d'une vague diminue en même temps que la profondeur de l'eau. En arrivant sur un rivage incliné, les nouvelles vagues rattrapent donc les anciennes, moins rapides, et leur font prendre de l'ampleur jusqu'à créer un état instable, qui se résout alors par le déferlement.
Critères de déferlement
Pour des vagues régulières qui se propagent, le déferlement résulte d'une instabilité qui se développe à partir de la crête des vagues dès que la vitesse des particules approche de la vitesse de phase de l'onde[1]. On trouve alors que la cambrure maximale d'une vague régulière est à peu près [2]. Dans cette formule, donnée par l'ingénieur Miche, H est la hauteur de la vague, L sa longueur d'onde et D la profondeur d'eau. Le facteur est justement le rapport entre l'amplitude de l'élévation et celle des vitesses orbitales en surface, en tout cas dans le cadre de la théorie des vagues linéaire. En eau profonde, le critère de Miche correspond au critère de Stokes pour les vagues de cambrure maximale: H/L=0,14. Par petits fonds, cela devient H/D=0.8: la hauteur des vagues est limitée par la profondeur.
Il est probable qu'un critère similaire sur la vitesse s'applique aux vagues irrégulières, en effet, une crête qui se déplace plus vite que la vitesse de phase conduit, si cet excès de vitesse dure assez longtemps, à l'écroulement de la crête sur la face avant. Les observations en laboratoire, montrent que des vagues déferlantes non stationnaires ont effectivement des vitesses qui s'approchent de la vitesse de phase.
Différentes formes du déferlement
Que ce soit en eau profonde ou sur le rivage, le déferlement résulte d'une convergence d'énergie qui augmente la densité locale de l'énergie au-delà de ce que la vague peut supporter. Plus cette convergence est rapide et plus de déferlement est intense. On différencie généralement le déferlement plongeant, très intense, du déferlement glissant, plus régulier.
Par petits fonds, c'est la pente du fond qui fait la vitesse de convergence de l'énergie. Ainsi une forte pente du fond donne plutôt un déferlement plongeant.
Simulation numérique
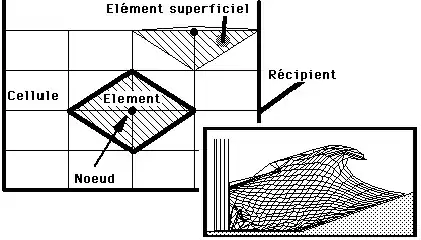
Le mouvement d'une vague créée dans un canal à houle par un générateur de vagues du type piston a été simulé sur microordinateur par un calcul de différences finies[3].
La méthode de calcul consiste à découper le volume fluide en quadrilatères où la pression et les autres paramètres sont constants et à diviser le temps en petits intervalles égaux. On associe à chaque nœud du maillage ainsi créé un élément obtenu en joignant entre eux les quatre nœuds voisins. On applique pour chaque pas de temps à cet élément les lois fondamentales de la mécanique qu'on intègre par différences finies au premier ordre. Le fluide est homogène, pesant et compressible. Le logiciel a été validé par comparaison avec des résultats expérimentaux et numériques issus de la littérature, concernant des vagues de moyenne amplitude. En faisant varier la profondeur et la vitesse du piston on a trouvé que la vitesse de la base de la vague ne dépend que de la profondeur mais que la vitesse de la crête est double de celle du piston.
Notes et références
- The stability of steep gravity waves, M. Tanaka, 1983:. J . Phys. Soc. Japan vol. 52, pp. 3047-3055
- Mouvements ondulatoires de la mer en profondeur croissante ou décroissante. forme limite de la houle lors de son déferlement. Application aux digues maritimes. Troisième partie. Forme et propriétés des houles limites lors du déferlement. Croissance des vitesses vers la rive, Miche 1944: Annales des Ponts et Chaussées, vol. Tome 114, pp. 369–406, 1944.
- [PDF]Schaeffer, B., Possibilités des microordinateurs - Simulation numérique d'une vague déferlante, dont le mouvement en profondeur et le profil sont calculés par microordinateur. Association Technique Maritime et Aéronautique, session 1988, Paris ATMA 88.
- Portail du monde maritime