Induction électrique
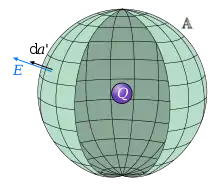
En électromagnétisme, l’induction électrique, notée , représente en quelque sorte la densité de charge par unité d'aire (en C/m²) ressentie en un certain point : par exemple, une sphère de rayon entourant une charge subit à cause d'elle en chacun de ses points un certain champ électrique, identique à celui qu'engendrerait la même charge uniformément répartie sur l'aire de la sphère. La densité de charge surfacique ainsi obtenue est alors l'intensité de l'induction électrique. Également nommée champ de déplacement électrique ou parfois improprement densité de flux électrique[1], cette dernière est en outre orientée perpendiculairement à la surface, dans le sens du champ électrique.
Ne doit pas être confondu avec Induction électromagnétique.
Pour les articles homonymes, voir Induction.
| Unités SI | C m−2 |
|---|---|
| Dimension | L −2·T·I |
| Base SI | s⋅A⋅m−2 |
| Nature | Grandeur vectorielle intensive |
| Symbole usuel | |
| Lien à d'autres grandeurs |
L'induction électrique, ainsi matérialisée par un vecteur en tout point de l'espace, forme donc un champ vectoriel dépendant de la position et du temps , et qu'on peut alors noter . Une possibilité alternative est la dépedance de l'induction électrique, alors notée , à la position dans l'espace et à la pulsation , qui apparaît dans les équations de Maxwell des milieux.
Dimension et unité
L'induction électrique est une grandeur vectorielle[2],[3]. De dimension L–2·T·I[2], elle est homogène à une excitation électrique[4] et une polarisation électrique[5]. Dans le Système international (SI) d'unités, elle s'exprime en coulombs par mètre carré (C/m2 ou C m−2)[2],[3].
Ce choix d'unités résulte du théorème de Gauss. Voir aussi Induction électrique dans un condensateur, infra.[précision nécessaire]
Relation avec le champ électromagnétique
En général, on considère les milieux dits linéaires, est alors relié au champ électrique par la relation
où :
- représente la permittivité absolue du milieu, qui est une matrice 3x3 dans les milieux anisotropes, et une fonction dans les milieux isotropes. Cette relation n'est pas universelle : échappent à cette relation, entre autres, les milieux électriquement non linéaires ( dépend alors aussi des termes quadratiques de ),
et les milieux dits « chiraux » ( dépend alors linéairement de mais aussi du champ magnétique ).
Induction électrique dans un condensateur
Pour un condensateur, la densité de charge sur les plaques est égale à la valeur du champ entre les plaques. Ceci résulte directement du théorème de Gauss, si on intègre sur une boîte rectangulaire chevauchant la surface d'une des plaques du condensateur :
où est l'élément d'aire orientée de la boîte et la charge accumulée par le condensateur. La partie de la boîte à l'intérieur de la plaque a un champ nul (donc la partie de l'intégrale s'y reportant est nulle), et sur les bords de la boîte, est perpendiculaire au champ (donc la partie de l'intégrale s'y reportant est aussi nulle). Finalement, il reste :
- ,
ce qui représente la densité de charge de la plaque.
Notes et références
- Le flux électrique étant l'intégrale d'un champ électrique sur une surface, cette expression est en effet équivalente au champ électrique lui-même ; l'induction éledctrique est au contraire plus proche d'une densité de charge.
- Dubesset 2000, s.v. induction électrique, p. 75.
- Taillet, Villain et Febvre 2018, s.v. déplacement électrique, p. 195, col. 2.
- Dubesset 2000, s.v. excitation électrique, p. 63.
- Dubesset 2000, s.v. polarisation électrique, p. 101.
Voir aussi
Bibliographie
- [Dubesset 2000] Michel Dubesset (préf. de Gérard Grau), Le manuel du Système international d'unités : lexique et conversions, Paris, Technip, coll. « Publications de l'Institut français du pétrole », , 1re éd., 1 vol., XX-169, ill., fig. et tabl., 15 × 22 cm, br. (ISBN 2-7108-0762-9, EAN 9782710807629, OCLC 300462332, BNF 37624276, SUDOC 052448177, présentation en ligne, lire en ligne), s.v. induction électrique, p. 75.
- [Favennec 2020] Pierre-Noël Favennec (dir.), Ondes électromagnétiques, t. Ier : Équations de Maxwell, propagation des ondes, Londres, ISTE, coll. « Sciences / Ondes / Électromagnétisme », , 1re éd., 1 vol., VII-292, ill. et fig., 16 × 24 cm, rel. (ISBN 978-1-78948-006-1, EAN 9781789480061, OCLC 122662970, BNF 46646869, SUDOC 25098184X, présentation en ligne, lire en ligne).
- [Taillet, Villain et Febvre 2018] Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Supérieur, hors coll. / sciences, , 4e éd. (1re éd. ), 1 vol., X-956, ill., fig., tabl. et index, 17 × 24 cm, br. (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, BNF 45646901, SUDOC 224228161, présentation en ligne, lire en ligne), s.v. déplacement électrique, p. 195, col. 2.
Articles connexes
Liens externes
- [OI] (en) « electric displacement » [« déplacement électrique »], notice d'autorité no 20110803095745843 de l'Oxford Index (OI), dans la base de données Oxford Reference de l'Oxford University Press (OUP).
- Portail de la physique
- Portail de l’électricité et de l’électronique