Dôme de Norton

Le dôme de Norton est une expérience de pensée construisant un système non-déterministe dans le cadre de la mécanique newtonienne, imaginée par John D. Norton (en) en 2003[1],[2]. C'est un cas particulier limite d'une classe plus générale d'exemples, dus à Sanjay Bhat et Dennis Bernstein en 1997[3]. Ce système peut être vu comme un problème de mathématiques ou de physique, mais pose aussi des questions philosophiques plus profondes[4],[5],[6],[7].

Coupe du dôme de Norton ; les unités sur les deux axes valent et l’ordonnée représente H=1-h.

Description

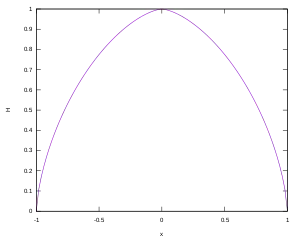
On s'intéresse, dans le cadre de la mécanique newtonienne, au mouvement d'un point matériel (une particule massive) initialement immobile au sommet d'un dôme dont la forme est une surface de révolution définie par la relation , où h est la différence d’altitude entre le point considéré et le sommet du dôme, r la distance géodésique du point au sommet, et g l'accélération de la pesanteur[6],[7].

Le principe fondamental de la dynamique montre que l'accélération tangentielle d'un point reposant sans frottement sur le dôme est alors [6] ; cette relation entre r et sa dérivée seconde est une équation différentielle du second ordre appelée équation du mouvement (avec conditions initiales ).

Solutions de l'équation

Norton montre qu'en dehors du cas où la particule reste immobile, les autres solutions correspondent à une immobilité durant un temps non déterminé, suivi d'un glissement dans une direction arbitraire. Le problème ne vient pas de cette seconde indétermination (une brisure spontanée de symétrie, dans le langage des physiciens), mais de ce que le mouvement semble se déclencher sans cause. Les équations de la mécanique newtonienne étant réversibles par rapport au temps, elles ont également pour solutions le même mouvement partant d'un lancer vers le sommet, où la particule s'immobilisera après un temps fini, mais c'est justement le fait que ce second mouvement parait naturel et le premier paradoxal qui constitue l’intérêt de cet exemple.

On peut remarquer au passage qu'un dôme de forme plus simple (par exemple une demi-sphère) ne fait pas apparaître la même difficulté, car alors il faudrait un temps infini pour atteindre le sommet avec une vitesse nulle[8] ; on rencontre le même phénomène en étudiant l'accostage d'un navire : s'il était possible d'atteindre en un temps fini un état de vitesse nulle, le mouvement inverse, où le navire s'éloignerait sans cause de l'état de repos serait possible ; c'est ce qui explique que le mouvement réel atteint le quai avec une vitesse non nulle, et qu'on a besoin en pratique d'amortisseurs (bouées ou pare-chocs d'accostage).

Résolution du paradoxe

D'un point de vue mathématique, le fait que l'équation différentielle correspondant au mouvement admette plusieurs solutions pour les mêmes conditions initiales contredit le théorème de Cauchy-Lipschitz, ce qui montre que les hypothèses de ce dernier ne sont pas vérifiées : la surface du dôme n'est pas deux fois continûment dérivable. Physiquement, on peut aussi traduire cela en disant qu'une telle surface est irréalisable en pratique (et comment faire pour poser un objet même ponctuel exactement au sommet ?), ou encore que les diverses simplifications du modèle newtonien (point matériel, surface sans frottement, etc.) ne sont pas réalistes. Mais d'un point de vue plus philosophique, cela amène également à une réflexion sur le déterminisme[6].

Références
  1. (en) John D. Norton, « Causation as Folk Science », Philosophers' Imprint, vol. 3, no 4,‎ , p. 1–22 (hdl 2027/spo.3521354.0003.004)
  2. (en) Jon Pérez Laraudogoitia, « On Norton's dome », Synthese, vol. 190, no 14,‎ , p. 2925–2941 (DOI 10.1007/s11229-012-0105-z)
  3. (en) Sanjay P. Bhat et Dennis S. Bernstein, « Example of indeterminacy in classical dynamics », International Journal of Theoretical Physics, vol. 36, no 2,‎ , p. 545–550 (ISSN 1572-9575, DOI 10.1007/BF02435747)
  4. Alexander Reutlinger, A Theory of Causation in the Social and Biological Sciences, Palgrave Macmillan, (ISBN 9781137281043), p. 109
  5. (en) Mark Wilson, « Determinism and the Mystery of the Missing Physics », The British Journal for the Philosophy of Science, vol. 60, no 1,‎ , p. 173–193 (DOI 10.1093/bjps/axn052, lire en ligne)
  6. (en) Samuel Craig Fletcher, « What counts as a Newtonian system? The view from Norton's dome », European Journal for Philosophy of Science, vol. 2, no 3,‎ , p. 275–297 (DOI 10.1007/s13194-011-0040-8, CiteSeerx 10.1.1.672.9952)
  7. (en) David B. Malament, « Norton’s Slippery Slope », Philosophy of Science, vol. 75, no 5,‎ , p. 799–816 (ISSN 0031-8248, DOI 10.1086/594525)
  8. (en) John Norton, « The Dome », sur www.pitt.edu (consulté le )

Articles connexes

Liens externes
  • Portail de la physique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.