Théorie des mécanismes
On entend par théorie des mécanismes[1] un ensemble de méthodes qui permettent d'étudier les mécanismes et les structures, en vue de les comprendre, de les améliorer ou de les concevoir. Ces méthodes reposent essentiellement sur deux branches de la mécanique, la statique et la cinématique[2], et cet article n'en abordera que les principaux aspects.
Pour les articles homonymes, voir Théorie des mécanismes (homonymie).
Le but de la théorie des mécanismes n'est pas d'établir une construction intellectuelle de plus, mais de donner aux techniciens et ingénieurs un outil de travail efficace. On ne s'étonnera donc pas de voir associées, aussi souvent que possible, des considérations pratiques avec des notions beaucoup plus abstraites.
Définitions préliminaires
- On appelle pièce tout sous-ensemble rigide faisant partie d'un mécanisme ou d'une structure, quelle que soit sa réalisation.
- Une liaison résulte de la mise en contact de deux pièces par l'intermédiaire de surfaces fonctionnelles appropriées. On attend d'une liaison qu'elle transmette certains efforts d'une pièce à l'autre, ou qu'elle interdise certains mouvements d'une pièce par rapport à l'autre. On dit bien « interdise » et non pas « autorise ».
- Les mécanismes et les structures résultent de l'agencement d'éléments rigides liés les uns aux autres ; ils comportent donc un nombre entier de pièces et un autre nombre entier, généralement différent, de liaisons. On trouve des systèmes dans lesquels certains éléments peuvent se mouvoir, une boîte de vitesses par exemple, et des agencements purement statiques comme l'ossature d'un bâtiment ou d'un ouvrage d'art, ou encore le montage qui immobilise une pièce en vue de son usinage sur une machine-outil.
- Dans un mécanisme formé de p + 1 pièces, on appelle généralement socle ou bâti celle qui sert de référence pour étudier, par la statique ou la cinématique, le comportement des p autres pièces.
Hypothèses et limites de l'étude
- Les pièces sont parfaitement indéformables : la distance de deux points quelconques A et B appartenant à une même pièce est donc rigoureusement invariable. On néglige ici l'élasticité, en déduisant immédiatement qu'un ressort ne doit jamais être considéré comme une pièce.
- Les surfaces fonctionnelles par lesquelles les pièces viennent en contact sont géométriquement parfaites. On néglige cette fois les tolérances de forme et d'état de surface.
- Les liaisons créées entre les pièces sont parfaites, c'est-à-dire qu'elles sont réalisées sans jeu, ni serrage, ni frottement. Les ajustements et l'usure sont exclus de l'étude.
Liaisons simples
Pour des raisons pratiques, les surfaces utilisées pour réaliser des liaisons sont le plus souvent des cylindres, des plans ou des sphères.
Les cylindres peuvent être réalisés très facilement et avec une bonne précision sur une large gamme de machines-outils, ce sont les surfaces les plus économiques et il faut bien sûr les utiliser aussi largement que possible. Les plans sont nettement moins faciles à réaliser, surtout s'ils ont une surface importante, mais ils restent d'un coût raisonnable. Les sphères sont les surfaces les plus onéreuses, surtout si l'on veut imposer à la fois un diamètre précis et des tolérances de forme et de rugosité très faibles. On les évite donc autant que possible en tant que telles, mais leur usage est indispensable pour obtenir certaines fonctions particulières ; dans ce cas, on essaie de trouver des solutions de substitution, ce qui est très souvent possible.
En associant deux à deux ces surfaces, on obtient six combinaisons qui correspondent aux six liaisons simples bien connues :
| association | liaison |
| plan et sphère | appui ponctuel, encore appelé « appui simple » |
| plan et cylindre | appui linéaire rectiligne, ou parfois « appui linéaire » tout court |
| plan et plan | appui plan |
| cylindre et sphère | appui linéaire annulaire, ou « anneau », ou encore « gouttière » |
| cylindre et cylindre | pivot glissant ou « verrou » |
| sphère et sphère | rotule ou « liaison sphérique » |
On ne s'attardera pas sur la liaison nulle (appelée liaison libre), ni sur la liaison complète (nommée liaison encastrement).
Chacune des liaisons simples possède des particularités qu'il convient de connaître par cœur si l'on veut utiliser efficacement la théorie des mécanismes. D'autres liaisons seront ajoutées par la suite et considérées comme des liaisons simples, moyennant certaines précautions.
Liaisons ponctuelles, linéiques et surfaciques
- contact ponctuel : en faisant se toucher une sphère et un plan, le contact théorique se résume à un point. En pratique, si la liaison doit transmettre des efforts, ce contact va s'écraser quelque peu et devenir une petite surface, sans quoi la pression serait infinie. L'appui ponctuel est cependant la plus précise de toutes les liaisons et la seule qui permette de localiser le contact réel dans une toute petite zone de l'espace. On ne s'en servira guère pour transmettre des efforts, sauf sous forme de contact roulant, en revanche on l'utilisera à chaque fois que l'on aura besoin de précision : transmission d'une information de position, construction d'appareils de mesure, montages de premier usinage, etc.
- contact linéique : on le rencontre dans les deux appuis linéaires, rectiligne et annulaire. Il supporte davantage d'efforts que le contact ponctuel, mais les imperfections des surfaces font que l'on ne connaît jamais avec précision les zones réelles dans lesquelles se font les portées entre les pièces.
- contact surfacique : on le trouve dans l'appui plan, le pivot glissant et la rotule. Pour l'obtenir, il faut deux surfaces complémentaires présentant des courbures opposées. En pratique les efforts transmis sont beaucoup plus importants que pour les contacts ponctuel et linéique, tandis que les zones réelles de portées sont toujours très mal déterminées. Ces liaisons seront donc refusées s'il faut transmettre des informations et au contraire recherchées pour transmettre des puissances.
Liaisons unilatérales et bilatérales
Une liaison unilatérale transmet certains efforts ou interdit certains mouvements dans un seul sens. Une liaison bilatérale qui transmet un effort transmet aussi l'effort opposé et de même, si elle interdit un mouvement, elle interdit également le mouvement opposé.
Les trois liaisons qui comportent un plan, c'est-à-dire l'appui ponctuel, l'appui linéaire rectiligne et l'appui plan, sont des liaisons unilatérales. Au contraire, l'appui linéaire annulaire, le pivot glissant et la rotule sont des liaisons bilatérales.
Une liaison unilatérale transmet les efforts dans un seul sens, et elle le fait alors sans jeu. Si les efforts changent de sens, elle n'existe plus. Une liaison bilatérale subsiste lorsque les efforts transmis changent de sens, mais le jeu se rattrape alors d'un côté ou de l'autre et les positions relatives des pièces ne sont plus déterminées avec une grande précision.
On raisonne souvent comme si les liaisons unilatérales étaient en fait bilatérales. Après tout, loger une sphère, un cylindre ou un « bloc » entre deux plans parallèles n'est pas vraiment plus difficile que d'ajuster deux sphères l'une à l'autre pour former une rotule.
Actions directes, efforts de liaison
Lorsque l'on étudie l'équilibre d'une pièce, il faut commencer par l'« isoler » et faire l'inventaire de tous les efforts extérieurs qu'elle subit. On s'aperçoit alors que ces efforts sont de deux sortes :
- les actions directes, appliquées autrement que par les liaisons et a priori connues ; on compte dans cette catégorie les forces de volume (poids, attractions électrique et magnétique), certaines forces de surface (pression d'un fluide, poussée du vent...), et celles que l'on applique volontairement (couple moteur, traction d'un ressort...),
- les efforts de liaison, qui sont les forces et les couples appliqués par les diverses pièces liées à celle que l'on étudie. Ces efforts sont a priori en partie inconnus.
Références centrées, degrés de liaison, degrés de liberté
Le mouvement d'une pièce P totalement libre dans l'espace par rapport au bâti peut être défini en un point par une vitesse linéaire et un taux de rotation. De même, une pièce totalement liée au bâti peut lui transmettre une action mécanique définie en un point par une force et un moment. Dans un cas comme dans l'autre, le mouvement et l'action mécanique peuvent prendre toutes les valeurs imaginables et pour les exprimer analytiquement, il faut six nombres algébriques dont chacun peut ne pas être nul. Dans le premier cas, tous les mouvements sont possibles, ce qui ne veut pas dire qu'ils aient effectivement lieu, c'est pourquoi on parlera de mouvements relatifs autorisés de P par rapport au bâti. Dans le second, tous les efforts peuvent être transmis, mais ils n'existent pas forcément, on parlera donc d'efforts transmissibles de P sur le bâti.
Références centrées
On prend maintenant pour exemple un mécanisme constitué d'une tige cylindrique montée dans un alésage du socle, donc liée à celui-ci par un pivot glissant.
On comprend facilement, compte tenu des hypothèses posées précédemment, que les particularités des mouvements autorisés et des efforts transmissibles par cette liaison ne dépendent ni de la longueur du cylindre selon lequel se fait le contact, ni de son diamètre, ni de sa position longitudinale, ni du fait que ce cylindre puisse être morcelé en plusieurs parties. On parle bien ici des particularités, pas des valeurs numériques. Pour les exprimer, il faut se référer à l'axe commun aux deux cylindres, qui constitue la référence centrée du pivot glissant.
Les références centrées sont en quelque sorte les « squelettes » des liaisons :
| liaison | références centrées |
| appui ponctuel | la normale commune aux deux surfaces, et pas seulement le point de contact comme on le pense généralement à tort |
| appui linéaire rectiligne | le plan normal aux deux surfaces qui passe par la droite de contact, et pas seulement cette dernière |
| appui plan | n'importe quelle normale aux plans, donc propriétés identiques dans tout l'espace ! |
| appui linéaire annulaire | l'axe du cylindre ET le centre de la sphère |
| pivot glissant | l'axe commun aux deux cylindres |
| rotule | le centre commun aux deux sphères |
On doit toujours garder cette liste présente à l'esprit !
Un système d'axes, un ensemble de notations, ne sont que des outils, qu'il faut choisir avec discernement, et seulement si l'on en a vraiment besoin. En les choisissant mal, on complique les problèmes d'une manière redoutable et l'on finit par échouer avec panache ! S'il faut utiliser un système d'axes, on ne le placera pas n'importe comment, on l'appuiera au contraire sur les références centrées des liaisons pour que les efforts ou les mouvements puissent être exprimés de la façon la plus simple possible.
Degrés de liaison, degrés de liberté
On prend ici le pivot glissant comme exemple ; il peut être étudié en statique ou en cinématique, peu importe, mais souvent il faut faire les deux études car on a besoin des ensembles de valeurs numériques qui définissent les efforts et les vitesses.
| en statique | en cinématique |
| Par hypothèse, la tige T doit rester en équilibre par rapport au bâti. Si nous lui appliquons une force dirigée suivant l'axe du pivot glissant ou un moment parallèle à cet axe, nous la faisons bouger ... et nous ne sommes plus en statique. Toutes les actions directes ne sont donc pas transmissibles au bâti et les inconnues sont les efforts de liaison. | L'étude cinématique des mécanismes fait toujours apparaître la solution banale du repos complet : toutes les vitesses sont nulles. Reste à savoir s'il existe une possibilité de mouvement de la tige T compatible avec les liaisons ; on cherche donc les 6 inconnues qui caractérisent le mouvement de la tige T par rapport au bâti. |
| Les forces dont les lignes d'action sont perpendiculaires à l'axe (on dit bien perpendiculaires, pas orthogonales) peuvent être transmises de la tige au socle sans engendrer de mouvement. Il en va de même pour tous les moments orthogonaux à l'axe.
L'ensemble des deux efforts transmissibles, force et moment, correspond à quatre valeurs algébriques indépendantes. Dans un problème de statique, ces quatre valeurs correspondent à quatre inconnues distinctes. Il existe par ailleurs deux valeurs algébriques correspondant à des actions directes qui doivent être nulles pour que l'on reste dans le domaine de la statique, la liaison n'est donc pas complète. |
Le pivot glissant autorise la rotation de la tige autour de l'axe, de même que la translation de la tige selon ce même axe. Ces deux mouvements sont indépendants et chacun peut donc prendre n'importe quelle valeur, ce qui ne fait guère avancer les choses, mais on sait que la liaison n'est pas complète.
En revanche, il est impossible de faire tourner la tige autour d'une direction orthogonale à l'axe, et de même les points de l'axe de la tige ne peuvent avoir aucun mouvement de translation perpendiculaire à celui-ci. Ces interdictions correspondent à 4 conditions imposées aux vitesses par 4 équations. |
On peut donner les deux définitions provisoires suivantes :
En écrivant l'équilibre de la tige par rapport au socle, on aurait 6 équations. Comme il n'existe que 4 inconnues, il y a donc 2 équations non principales qui doivent être rendues compatibles avec le système, sinon celui-ci est impossible ... on n'est plus en statique. |
On peut donner les deux définitions provisoires suivantes :
Avec 4 équations seulement, il est impossible de déterminer les 6 inconnues qui pourraient définir le mouvement de la tige. Il existe donc 2 inconnues non principales qui, n'étant pas imposées par les équations, deviennent de simples paramètres pouvant prendre n'importe quelle valeur. |
| Il y a donc ici ns = 4 degrés de liaison et nc = 2 degrés de liberté.
Pour toutes les liaisons simples, on trouve toujours ns + nc = 6. | |
Il faut toujours garder à l'esprit les valeurs caractéristiques des diverses liaisons simples !
| liaison | ns | nc |
| appui ponctuel | 1 | 5 |
| appui linéaire rectiligne | 2 | 4 |
| appui plan | 3 | 3 |
| appui linéaire annulaire | 2 | 4 |
| pivot glissant | 4 | 2 |
| rotule | 3 | 3 |
Nouvelles définitions, familles de mécanismes
- lorsque deux pièces sont liées par au moins deux liaisons simples, on parle de liaison composée. Exemples : une roue folle montée sur une portée cylindrique et en appui contre un épaulement, un vilebrequin de moteur lié au bâti par 5 paliers, etc.
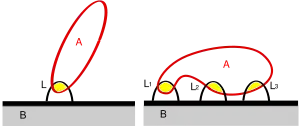
- une chaîne continue ouverte est une succession de pièces dont chacune est liée à la précédente par une liaison simple. On a donc, en décomptant le bâti, p pièces reliées par a = p liaisons. Exemples : un bras de pelle mécanique, un doigt par rapport à la main, etc.
- une chaîne continue fermée est constituée de manière analogue, sauf que les pièces forment une boucle. Toujours en décomptant le bâti, on trouve p pièces et a = p + 1 liaisons. Cette disposition est très fréquente dans les systèmes de transformation de mouvement, on trouve par exemple p = 2 et a = 3 dans le cas d'un réducteur de vitesse comportant un carter, un arbre lent et un arbre rapide.
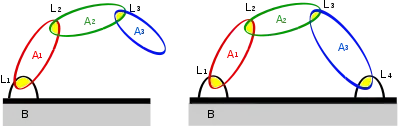
- un mécanisme complexe comporte un ensemble de pièces liées de façon plus compliquée que dans les cas précédents. Schématiquement, en considérant l'ensemble carter + vilebrequin à 5 paliers + bielles + pistons d'un moteur à 4 cylindres, on trouve par exemple p = 9 pièces et a = 13 liaisons simples ou composées.
Notion d'isostaticité ou de « non surabondance »
Pour immobiliser une pièce A par rapport à un bâti B, ou pour transmettre tout type d'effort de A à B, ce qui revient au même, on peut penser qu'il faut créer entre A et B une liaison composée telle que la somme Ns des degrés de liaison introduits par les liaisons simples qui la composent soit égale à 6
Il existe beaucoup de solutions, comme :
- un pivot glissant et un appui linéaire rectiligne,
- une rotule associée à un appui linéaire annulaire et un appui ponctuel,
- trois appuis linéaires rectilignes,
- etc.
La condition Ns = 6, comme on le verra, est nécessaire mais pas suffisante !
La liaison bien connue « point trait plan » de Lord Kelvin, qui introduit les six degrés de liaison à l'aide de six appuis ponctuels, répond à cette condition.

La sphère 3 repose dans un trièdre creux, ce qui impose la position de son centre par rapport au bâti mais autorise encore les trois rotations de A par rapport au bâti. En appuyant la sphère 2 dans un « vé », on fixe un second point, de sorte que A ne peut plus tourner qu'autour de l'axe passant par les centres des deux sphères. L'appui de la sphère 1 sur un plan achève l'immobilisation.
Il existe donc suffisamment d'appuis, mais pas trop. En rajouter un ne permettrait pas d'avoir une meilleure immobilisation, ou de mieux transmettre les actions directes au bâti, tandis qu'en supprimer un rendrait la pièce A mobile par rapport à B, ou empêcherait de transmettre certains efforts au bâti.
On peut bien sûr vérifier tout cela par le calcul.
| du point de vue de la statique | du point de vue de la cinématique |
| L'équilibre de la pièce A par rapport au bâti B donne 6 équations et chaque appui ponctuel transmet une force inconnue ayant pour ligne d'action sa normale, ce qui donne un système « carré » de 6 équations linéaires à 6 inconnues.
Si tout se passe bien, ce système a une solution et les 6 équations imposent les valeurs des 6 inconnues. On en tire deux conclusions :
|
Les 6 inconnues s'appliquent au mouvement de la pièce A par rapport au bâti B. Chaque appui ponctuel interdit la translation de A par rapport à B dans la direction de sa normale, ce qui se traduit par une équation. Les 6 appuis donneront donc en tout 6 équations, ce qui donne un système « carré » de 6 équations linéaires à 6 inconnues.
Si tout se passe bien, ce système a une solution autre que la solution banale (toutes les vitesses nulles) et les 6 équations imposent les valeurs des 6 inconnues. On en tire deux conclusions :
|
| Du point de vue des mathématiques, on dira avec plus de précision : | |
| On trouve un système de 6 équations linéaires à 6 inconnues avec second membre. Si son déterminant principal est d'ordre 6, son rang est égal à 6, toutes les inconnues et toutes les équations sont principales.
Toutes les équations étant principales, la pièce A est immobilisée, quelles que soient les valeurs des actions directes qu'elle reçoit, la liaison est complète. Toutes les inconnues étant principales, les 6 forces d'appui sont déterminées, la liaison composée est isostatique. |
On trouve un système homogène de 6 équations linéaires à 6 inconnues. Si son déterminant principal est d'ordre 6, son rang est égal à 6, toutes les inconnues et toutes les équations sont principales.
Toutes les équations étant principales, aucune liaison ne fait double emploi avec les autres, de sorte que la liaison n'est pas surabondante. Toutes les inconnues étant principales, les 6 valeurs définissant le mouvement de la pièce A sont nulles, la liaison est complète. |
| Un système est dit isostatique, ou non surabondant,
lorsque tous les efforts de liaison sont déterminés, ou lorsqu'aucune liaison ne fait double emploi avec les autres. | |
On pourrait évidemment trouver des situations où les choses ne seraient pas aussi simples, par exemple si les normales de deux ou plusieurs appuis étaient parallèles, ou si toutes les normales étaient concourantes.
La liaison de Lord Kelvin est intéressante pour positionner des pièces de façon fidèle. Quelle que soit la précision avec laquelle les diverses surfaces ont été réalisées, un instrument de mesure porté par la pièce A reviendra toujours dans la même position, si celle-ci est retirée du socle puis remise en place.
Comme on n'utilise que des liaisons unilatérales, la liaison ne présente aucun jeu, mais certains efforts appliqués sur la pièce A peuvent la déboîter. Il suffit pour éviter cet inconvénient d'ajouter une bride ou un ressort pour la maintenir en place.
Les trois sphères peuvent aussi être appuyées dans trois rainures en forme de V, ce qui donne la liaison de Boys, moins connue et moins utilisée que celle de Lord Kelvin. On peut la réaliser de façon qu'elle présente une symétrie d'ordre 3, ce qui peut être aussi bien un avantage qu'un inconvénient, selon les circonstances.
L'ablocage des pièces en vue de leur premier usinage se fait par six appuis portant sur des surfaces brutes et permettant une immobilisation isostatique. Lors des usinages ultérieurs, on s'appuie sur les surfaces déjà usinées et jamais uniquement sur de nouvelles surfaces brutes. Dans une gamme d'usinage, une « reprise sur brut » conduit toutes les pièces en file indienne droit dans la poubelle !
Notion de mobilité, notion d'hyperstaticité ou de surabondance
Au lieu d'utiliser des appuis ponctuels, on envisage maintenant de réaliser la liaison complète d'une pièce A par rapport à un bâti B en associant deux rotules. Chacune d'elles apportant 3 degrés de liaison, cela en fait 6 en tout, donc juste ce qu'il faut ... Il va donc falloir usiner deux sphères sur chaque pièce, puis procéder à l'assemblage.
Ici deux solutions apparaissent, selon que ces sphères seront concentriques ou non. Pour éviter de se trouver tout de suite dans un cas particulier, on peut choisir la solution la plus générale et faire en sorte que les centres ne soient pas confondus :

En statique, l'équilibre de la pièce A fournit 6 équations, tandis que les deux rotules apportent autant d'inconnues qu'il y de degrés de liaison en tout, c'est-à-dire 6.
En cinématique, les deux rotules imposent 6 conditions au mouvement, autant qu'il y a de degrés de liaison en tout, on pourra donc écrire 6 équations qui contiendront 6 inconnues qui correspondent au mouvement général de la pièce A par rapport au bâti B.
On peut bien sûr étudier ce problème de façon entièrement mathématique mais ce n'est sans doute pas nécessaire pour que l'on comprenne très vite qu'il y a un gros ennui. La pièce A n'est pas complètement liée au bâti, elle peut tourner autour d'un axe qui passe par les centres des deux rotules, si on lui applique des actions extérieures comportant un moment parallèle à cet axe. Par ailleurs, on se rend compte aussi que l'assemblage va dépendre de la distance des centres des sphères, qui doit être la même sur les deux pièces (on rappelle que les liaisons sont parfaites, mais ici cela ne suffit pas à permettre l'assemblage, il faut encore voir la cotation de position). Que s'est-il passé ?
| point de vue de la statique | point de vue de la cinématique |
| Le système de 6 équations qui traduit l'équilibre de la pièce A par rapport au bâti est tel que 5 de ces équations imposent les valeurs de 5 inconnues ; il existe donc une équation surnuméraire et la sixième inconnue est indéterminée. Pour que le système d'équations ne soit pas impossible, c'est-à-dire pour que l'on reste en statique, la 6e équation doit être compatible avec les autres.
Si ces équations sont correctement écrites, tous les termes où figurent des inconnues sont dans les premiers membres et ceux qui contiennent les valeurs des actions directes dans les seconds membres. La compatibilité de la 6e équation impose une condition aux seconds membres, l'une des valeurs des actions directes est imposée. Ici, tout moment appliqué à la pièce A parallèlement à l'axe qui passe par le centre des rotules doit être nul. |
Le système de 6 équations qui traduit l'ensemble des mouvements interdits de la pièce A par rapport au bâti est redondant, autrement dit, l'un des mouvements est interdit deux fois. Il s'ensuit qu'un autre mouvement ne peut plus l'être du tout ; par conséquent, la liaison composée ne peut en aucun cas être complète puisque seulement 5 des 6 inconnues sont déterminées, et en l'occurrence nulles.
On vérifierait facilement que la 6e inconnue, qui correspond au taux de rotation autour de l'axe qui passe par les centres des rotules, ne figure même pas dans les équations. |
| Il apparaît donc une mobilité puisque si ce moment n'est pas nul, la pièce A tourne par rapport au bâti. | Il apparaît donc une mobilité puisque rien n'empêche la pièce A de tourner par rapport au bâti. |
| La pièce A présente un degré de mobilité par rapport au bâti B,
c'est-à-dire que son mouvement éventuel peut être caractérisé par une valeur numérique indépendante. Pourquoi parler de mobilité alors qu'existe déjà la notion de liberté ? Tout simplement parce que les degrés de liberté caractérisent les liaisons et les degrés de mobilité, les pièces. Il est donc impératif de distinguer ces deux concepts fondamentalement différents par deux termes différents. | |
| L'inconnue non déterminée correspond à un effort transmissible excédentaire, ce qui correspond à une condition géométrique impérative. En théorie, il est en effet rigoureusement impossible d'assembler les deux pièces A et B si la distance des centres des sphères n'est pas strictement identique sur les deux pièces.
En pratique, les miracles n'existent pas et cette identité rigoureuse ne peut jamais être réalisée. Le montage direct des deux pièces ne peut donc se faire que moyennant des déformations d'autant plus importantes que l'écart entre les deux distances est plus important ; bien sûr, ces déformations sont provoquées par des forces opposées dont la ligne d'action n'est autre que la droite qui passe par les centres des rotules. L'une des pièces est « étirée » et l'autre « comprimée », sans que l'on puisse déterminer les valeurs algébriques de ces forces. |
L'équation excédentaire traduit le fait qu'un mouvement est interdit deux fois ; il s'agit de la translation de la pièce A par rapport à la pièce B dans la direction de la droite qui passe par les centres des deux rotules.
Cette double interdiction correspond à une condition géométrique impérative. En théorie, il est en effet rigoureusement impossible d'assembler les deux pièces A et B si la distance des centres des sphères n'est pas strictement identique sur les deux pièces. En pratique, les miracles n'existent pas et cette identité rigoureuse ne peut jamais être réalisée. Le montage direct des deux pièces ne peut donc se faire que moyennant des déformations d'autant plus importantes que l'écart entre les deux distances est plus important. |
| La liaison composée présente un degré d'hyperstaticité, . | La liaison composée présente un degré de surabondance. |
| Une liaison hyperstatique ou surabondante de degré 1 comporte un degré de liaison de plus que ce qu'il faudrait pour assurer exactement la transmission des efforts au bâti ou pour interdire tous les mouvements relatifs indésirables.
Ce degré de liaison excédentaire correspond à une condition géométrique indépendante qu'il faudra traduire en pratique sous forme de prescriptions chiffrées pour que les pièces puissent être assemblées dans de bonnes conditions. La théorie des mécanismes a donc des conséquences directes sur la cotation de position qui définit, sur chaque pièce, les relations entre les surfaces fonctionnelles. Les conséquences de l'hyperstaticité ou de la surabondance se font surtout sentir en statique, car en général les efforts indéterminés nuisent gravement à la longévité et à la fiabilité des montages. Pour les éviter, il faut usiner les pièces avec une précision d'autant plus grande qu'elles sont moins déformables ; si c'est impossible, il devient impératif de prévoir des éléments de réglage. Dans les deux cas, cela aboutit à des montages plus coûteux, éventuellement plus lourds et plus encombrants, et toujours plus difficiles à entretenir. | |
| Du point de vue des mathématiques, on dira avec plus de précision : | |
| En écrivant l'équilibre de la pièce A par rapport au bâti B, on aboutit à un système de 6 équations linéaires à 6 inconnues.
Ce système est de rang 5 et comporte donc 5 équations principales qui déterminent les valeurs de 5 inconnues principales. La compatibilité de l'équation non principale impose une condition sur les seconds membres, c'est-à-dire sur les actions directes. Elle correspond à un degré de mobilité, à savoir la rotation de la pièce A par rapport au bâti B autour d'un axe qui passe par les centres des deux rotules. L'inconnue non principale correspond à un effort indéterminé, donc à un degré d'hyperstaticité ; il est impossible de connaître la force de serrage qui s'exerce entre les pièces, lors du montage, selon la droite qui passe par les centres des rotules. Il existe une condition géométrique à respecter pour permettre l'assemblage : la distance entre les centres des sphères doit être rigoureusement identique sur les deux pièces. |
En écrivant la compatibilité du mouvement de la pièce A par rapport au bâti B, on aboutit à un système homogène de 6 équations à 6 inconnues.
Ce système est de rang 5 et comporte donc 5 équations principales qui déterminent les valeurs de 5 inconnues principales. L'équation non principale correspond à un mouvement interdit de façon redondante, donc à un degré de surabondance. Il existe une condition géométrique à respecter pour permettre l'assemblage : la distance entre les centres des sphères doit être rigoureusement identique sur les deux pièces. L'inconnue non principale correspond à un mouvement qui n'est interdit par aucune liaison, donc à un degré de mobilité, à savoir la rotation de la pièce A par rapport au bâti B autour d'un axe qui passe par les centres des deux rotules. |
En résumé, la liaison composée de deux rotules dont les centres sont distincts est caractérisée par :
| |
Cette liaison peut correspondre, par exemple, au montage d'un arbre sur deux roulements à rouleaux coniques. Certaines pièces de ces roulements sont en effet légèrement bombées, généralement la cuvette (bague extérieure) de façon à permettre un léger « rotulage » permettant un fonctionnement correct malgré les défauts d'usinage, d'alignement, de montage et les déformations des pièces sous charge. Ce rotulage varie, selon les types de roulement, de 2' à 10' d'angle. Tant que cette limite n'est pas atteinte, et si le roulement est maintenu emboîté, il se comporte comme une rotule. Si elle est dépassée, alors les contacts ne se font plus dans les conditions prévues et la détérioration rapide est inévitable.
Si l'on assemblait sans précautions spéciale un arbre monté sur deux roulements à rouleaux coniques, en mettant tous les éléments en butée contre des épaulements, on verrait apparaître un jeu ou un serrage. Dans le premier cas, les roulements deviendraient bruyants, la précision du guidage ne serait plus assurée et les roulements déboîtés ne dureraient pas longtemps. Dans le second, le serrage pourrait être insuffisant, les roulements se déboîteraient alors sous charge, ou trop important, ce qui engendrerait des pressions de contact trop élevées, un échauffement excessif et une détérioration rapide. À moins d'utiliser, dans des conditions précises, des roulements appairés, la meilleure solution consiste à installer des éléments de réglage qui permettront de soumettre les roulements à une précharge bien contrôlée. Cette précharge doit au moins éviter que les roulements se déboîtent sous l'effet des efforts liés au fonctionnement et elle permet, pour les applications de précision, d'augmenter la raideur des paliers qui se comportent toujours plus ou moins, en pratique, comme des liaisons élastiques.
Définitions, remarques et observations
Degrés de liberté
- On ne retrouve jamais les degrés de liberté, sous quelque forme que ce soit, dans les équations d'équilibre en statique ou dans les relations de compatibilité des mouvements en cinématique, en fait, leur utilisation se cantonne à appuyer une éventuelle description qualitative d'un système.
- Dans beaucoup d'esprits, le cas du système vis-écrou pose problème. En effet, la vis peut avancer par rapport à l'écrou dans la direction de l'axe et tourner autour de l'axe. Il existe donc deux mouvements relatifs possibles mais ces mouvements ne sont pas indépendants puisque la vitesse de translation et la vitesse de rotation sont toujours liées. Ainsi, la liaison hélicoïdale introduit 5 degrés de liaison et un seul degré de liberté et non deux.
Degrés de mobilité
- un degré de mobilité correspond à un mouvement indépendant d'une pièce ou d'un groupe de pièces.
Dans l'exemple ci-dessous, sous réserve évidemment que les liaisons n'arrivent pas en butée, il existe 3 degrés de mobilité : la rotation de la pièce « rouge » autour de l'axe A qui passe par les centres des rotules 1 et 2, la rotation de la pièce « bleue » autour de l'axe B qui passe par les centres des rotules 2 et 3, mais aussi la rotation simultanée des pièces « rouge » et « bleue » autour de l'axe C qui passe par les centres des rotules 1 et 3. Cette dernière rotation subsiste, par exemple, si l'on remplace la rotule 2 par une soudure.
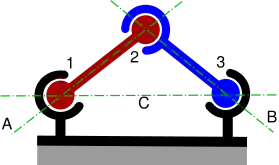
Les trois vitesses de rotations sont absolument indépendantes les unes des autres, elles peuvent prendre n'importe quelle valeurs et se produire séparément ou simultanément.
- Il est absolument impossible de trouver le nombre des degrés de mobilité des pièces en utilisant les degrés de liberté introduits par les liaisons.
Degrés d'hyperstaticité
- Un degré d'hyperstaticité est nécessairement accompagné d'une condition géométrique correspondante. Imposer une condition géométrique n'a de sens que si on peut la mesurer. Les conditions géométriques complexes se ramènent toujours à deux sortes de conditions géométriques élémentaires dont chacune est relative à une distance ou à un angle. Par exemple, la perpendicularité d'un axe avec un plan représente deux conditions élémentaires, puisqu'il faut vérifier que l'angle de l'axe et du plan est droit dans deux directions différentes. Le parallélisme de deux plans suppose que l'on mesure les distances a, b et c de trois points d'un plan par rapport à l'autre et que l'on vérifie que a = b = c, ce qui fait deux conditions ; si de plus la distance des deux plans est imposée, cela fait une troisième condition. Pour vérifier qu'un point se trouve bien sur un axe, il faut effectuer deux mesures. Et ainsi de suite ...
- Il est absolument impossible de trouver le nombre des degrés d'hyperstaticité des pièces en utilisant les degrés de liberté introduits par les liaisons.
- Une liaison en chaîne continue ouverte n'est jamais hyperstatique.
- Dans une chaîne continue fermée, le degré d'hyperstaticité ne peut pas dépasser 6.
Expression des résultats d'une étude
- Les résultats d'une étude ne doivent pas s'exprimer en fonction des outils de modélisation qui y ont été utilisés.
En effet, on comprend facilement que la température d'un objet ne doit pas dépendre du thermomètre qui a servi à la mesurer. De même, les propriétés d'un mécanisme dépendent de ce mécanisme lui-même et absolument pas de la façon dont on l'a étudié, ni des outils que l'on a utilisé pour l'étude. C'est pourquoi on ne doit jamais tirer des conclusions comme « la pièce A tourne autour de l'axe Ox », mais par exemple « la pièce A peut tourner par rapport au bâti B autour de l'axe qui passe par les centres des rotules 1 et 2 » ou encore « la pièce A peut coulisser par rapport à la pièce C dans la direction parallèle au plan de l'appui linéaire rectiligne 1 et à l'axe de la liaison linéaire annulaire 2 »
- On notera ici que le mouvement d'un solide ne peut être défini que par rapport à un autre système matériel de référence et qu'il doit rester compatible avec les surfaces fonctionnelles utilisées pour réaliser les liaisons qui constituent le mécanisme étudié.
Hypostatisme
On utilise parfois le terme hypostatisme lorsqu'un système possède des mobilités internes dites "parasites", c'est-à-dire pouvant nuire au bon fonctionnement de celui-ci.
Cependant, il n'existe pas de définition rigoureuse associée à ce terme, son utilisation est donc restreinte à des fins de vulgarisation.
Généralisation aux mécanismes complexes, formule fondamentale
D'une manière générale, un mécanisme comporte p pièces liées par a liaisons simples ou assimilées introduisant un nombre total Ns de degrés de liaison (ou Nc = 6a – Ns degrés de liberté, mais ce nombre-là n'a guère d'importance).
| étude générale en statique | étude générale en cinématique | |
| L'équilibre des p pièces conduit théoriquement à écrire un système de 6p équations linéaires à Ns inconnues. | La compatibilité des mouvements des p pièces avec les liaisons conduit théoriquement à écrire un système homogène de Ns équations linéaires à 6p inconnues. | |
En pratique, les nécessités du paramétrage imposent souvent d'écrire un nombre λ d'équations et d'inconnues supplémentaires, de sorte que l'on a finalement :
|
En pratique, les nécessités du paramétrage imposent souvent d'écrire un nombre µ d'équations et d'inconnues supplémentaires, de sorte que l'on a finalement :
| |
Le rang du système d'équations est rs, il y a donc :
|
Le rang du système d'équations est rc, il y a donc :
| |
On trouve forcément les mêmes valeurs pour :
| ||
| On élimine rs entre les nombres d'équations et d'inconnues
rs = 6p + λ – d = Ns + λ – h d'où h = Ns – 6p + d |
On élimine rc entre les nombres d'équations et d'inconnues
rc = Ns + µ – h = 6p + µ – d d'où h = Ns – 6p + d | |
On arrive évidemment à la même relation dans les deux cas :
Cette formule générale est un instrument essentiel dans beaucoup d'études de mécanismes. Elle ne remplace pas d'autres outils, dans la mesure où elle permet de compter les degrés mais sans en préciser la nature. Elle est absolument fondamentale dans les processus de création de mécanismes nouveaux. Il faut aussi noter que pour un mécanisme donné, si le degré d'hyperstaticité varie d'une certaine quantité, le degré de mobilité varie également de la même quantité. | ||
La grandeur 6p – Ns est parfois appelée « nombre de Grübler » (anglais : Gruebler count).
Mobilité utile, mobilité interne, problèmes de précision
Premier exemple
L'appui ponctuel d'une pièce A sur un bâti B engendre toujours des pressions de contact très élevées et on ne peut donc pas l'utiliser pour transmettre des efforts importants, surtout dans le cas où un glissement peut avoir lieu. L'idée de le remplacer par un mécanisme un peu plus complexe, remplissant exactement la même fonction, mais ne mettant en jeu que des liaisons surfaciques, aboutit à diverses solutions que l'on peut trouver en utilisant à bon escient la formule générale h = Ns - 6p + d. Parmi les solutions possibles, on peut ajouter une pièce intermédiaire I pour obtenir une liaison en chaîne continue ouverte selon le schéma ci-dessous :

- une chaîne continue ouverte n'étant jamais hyperstatique, h = 0. ce n'est pas étonnant, il n'y a aucune condition de montage particulière,
- l'appui plan introduit 3 degrés de liaison, il en va de même pour la rotule, donc Ns = 6,
- comme on a deux pièces liées au bâti, 6 p = 12.
On a donc 0 = 6 - 12 + d, ce qui donne bien évidemment d = 6 degrés de mobilité.
Si la pièce A était liée au bâti par un appui ponctuel « ordinaire », on aurait 0 = 1 - 6 + d, ce qui lui donnerait d = 5 degrés de mobilité. Avec la pièce intermédiaire, elle n'a pas davantage de mobilités, sinon elle serait complètement libre dans l'espace, il est facile de voir que ses mouvements sont exactement ceux que permettrait un appui ponctuel. Naturellement, le 6e degré de mobilité se retrouve quelque part et cela ne peut être qu'au niveau de la pièce intermédiaire I ; celle-ci peut en effet tourner autour d'un axe perpendiculaire au plan d'appui et passant par le centre de la rotule.
La pièce intermédiaire I peut aussi se déplacer en translation dans deux directions de l'espace, mais ces mouvements sont liés aux deux translations possibles de la pièce A et ils ne sont donc pas indépendants. D'ailleurs, si l'on soudait la pièce A au bâti B, ces translations seraient supprimées tandis que la rotation subsisterait.
On convient donc de distinguer deux sortes de mobilités, en fonction de l'usage prévu pour les éléments du mécanisme :
- les mobilités utiles sont celles qui font que le mécanisme remplit les fonctions prévues ; il s'agit ici des cinq mobilités de la pièce A, deux translations et trois rotations possibles,
- les mobilités internes n'ont aucun rôle fonctionnel ; ici il n'y en a qu'une, la rotation de la pièce A définie plus haut.
Faut-il supprimer les mobilités internes, ou bien peut-on s'en accommoder ? La réponse est avant tout d'ordre technologique et dépend donc des besoins et du contexte. Ici, la rotation de la pièce I n'a strictement aucune influence sur le mouvement et la précision du positionnement de la pièce A, a priori on n'a pas besoin de s'en préoccuper outre mesure.
Deuxième exemple
Comme précédemment, on peut chercher à remplacer une liaison linéaire annulaire par une liaison en chaîne continue ouverte n'utilisant que des liaisons surfaciques. L'une des solutions possibles utilise un pivot glissant et une rotule :
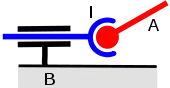
La pièce A doit posséder les 4 degrés de mobilité utiles qu'elle aurait dans le cas d'une liaison linéaire annulaire directe, ce que l'on vérifiera facilement ici. La formule magique donne cependant :
h = 0 = (4 + 3) - 12 + d, d'où d = 5
Il existe là aussi une mobilité interne évidente, la pièce intermédiaire peut tourner autour de l'axe des cylindres. Cependant, la situation est loin d'être la même que dans le cas précédent, car cette mobilité interne peut nuire à la précision du mécanisme.
Dans le premier exemple, en associant sur la pièce intermédiaire un plan et une sphère, il n'existe qu'un seul cas de figure : la distance du centre de la sphère au plan est fixée une fois pour toutes et impose la distance du centre de la sphère réalisée sur la pièce A au plan d'appui usiné sur le bâti B.
Cette fois, les choses sont très différentes puisque nous avons une alternative : en effet, le centre de la sphère réalisée sur la pièce intermédiaire peut se trouver sur l'axe du cylindre, mais aussi en dehors :
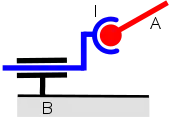
Dans cette situation, la mobilité interne de la pièce I est supprimée tandis que la pièce A voit sa mobilité passer de 4 à 5 degrés. La chaîne continue ouverte est donc équivalente à un appui ponctuel, en effet, tout se passe comme si la sphère réalisée sur la pièce A était en contact extérieur avec un cylindre réalisé sur le bâti ; la pièce intermédiaire ne tourne autour de l'axe du pivot glissant que si elle est mise en mouvement par la pièce A et il est clair que si celle-ci est « soudée » au bâti, plus rien ne bouge.
Idéalement, le remplacement d'une liaison linéaire annulaire par la chaîne continue ouverte proposée nécessite une position précise pour les deux surfaces réalisées sur la pièce intermédiaire : le centre de la sphère doit se trouver très exactement sur l'axe du cylindre. En pratique, même en prenant toutes les précautions voulues, cette coïncidence sera toujours soumise à tolérance et donc seulement approchée.
La question qui se pose donc ici est la suivante : que se passe-t-il lorsque le centre de la sphère est à peu près sur l'axe du cylindre ? Tout d'abord, il n'est pas possible en pratique de faire tourner la pièce intermédiaire en se servant de la pièce A comme d'une manivelle. Si on la saisit directement pour la faire tourner sans provoquer sa translation, le centre de la sphère usinée sur la pièce A décrit un très petit cercle. La position exacte de ce point dépend donc de l'angle de rotation de la pièce intermédiaire et de ce fait, la mobilité interne a une influence directe sur le positionnement de la pièce A et donc sur la précision du mécanisme. Si l'on veut améliorer cette précision, il faut donc ajouter un degré de liaison quelque part afin de supprimer non pas un mouvement indésirable, mais une possibilité de mouvement indésirable. La solution qui vient naturellement à l'esprit est de transformer le pivot glissant en glissière, mais ce n'est pas la seule possible.
Problèmes de contacts et « machines à coincer »
Une sphère tangente à deux plans parallèles permet d'obtenir deux points de contact dont les normales sont confondues. On obtient ainsi l'équivalent d'un appui ponctuel bilatéral.
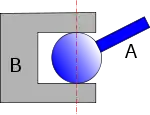
Il ne faut pas oublier qu'il s'agit en fait d'une liaison composée de deux appuis ponctuels et qu'il existe un degré d'hyperstaticité : h = (1 + 1) - 6 + 5 = 1.
La condition géométrique à respecter pour que le montage soit possible est évidemment très simple, la distance des plans doit être égale au diamètre de la sphère.
Lorsque les deux surfaces bombées n'appartiennent pas à la même sphère, l'hyperstaticité se manifeste immédiatement. Si le dispositif a l'allure schématisée ci-dessous, la distance des plans est supérieure au diamètre des sphères et la fonction est remplie tant que les éléments restent dans une position telle que les deux contacts ont la même normale. En revanche, si la pièce A bascule, le contact ne peut plus être maintenu des deux côtés du bâti en même temps. Le contact se produit d'un côté ou de l'autre et la liaison prend du jeu.
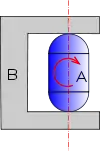 ..... devient .....
..... devient ..... 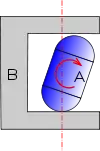
Si maintenant la distance des plans est plus petite que le diamètre des sphères, le comportement est très différent. Lorsque les deux contacts ont la même normale, aucun effort ne peut s'opposer au basculement, mais dès que celui-ci a commencé, il ne peut pas se poursuivre.
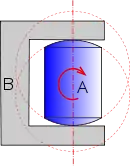
En pratique, les pièces n'étant pas rigoureusement indéformables, les deux normales peuvent se décaler, le basculement se produit mais il est très vite freiné par des efforts de contact d'autant plus importants que les pièces sont plus rigides. La pièce A ne peut plus se déplacer entre les plans à cause du frottement, elle est alors littéralement coincée. Le mécanisme lui-même est en danger de déformation permanente ou de rupture.
La conclusion est la même si on inverse le sens des contacts, sauf que cette fois le coincement est plus facile à imaginer et qu'il se produit quels que soient les rayons des sphères.
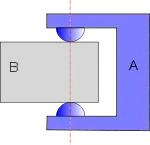
Problèmes de représentation mentale et de schématisation
Nature du problème
Il est relativement facile de comprendre et d'étudier un mécanisme existant, à partir d'un plan ou d'une réalisation concrète. En revanche, il est souvent beaucoup plus délicat de se représenter mentalement un mécanisme, lorsque l'on recherche la solution d'un problème et que celle-ci n'a pas été dessinée ni a fortiori réalisée.
La formule magique h = ns - 6 p + d suggère, lorsqu'on la sollicite, des combinaisons de liaisons susceptibles de remplir une fonction définie à l'avance, mais ce petit jeu nécessite une certaine gymnastique intellectuelle. En effet, cette formule amène à compter des degrés de liaison mais ce décompte ignore la nature de ces degrés ; or, celle-ci doit impérativement être prise en compte lors de l'étude critique de telle ou telle solution éventuelle.
Les concepteurs dotés de grandes facilités de représentation mentale passeront en revue les diverses possibilités et seront capables de faire très vite un tri exhaustif entre ce qui ne peut pas fonctionner, ce que l'on peut retenir à la rigueur et ce qui a toutes les chances de donner un mécanisme satisfaisant à la fois sur le plan technique et sur celui du coût de revient.
Les autres devront raisonner de façon plus laborieuse et il leur faudra sans doute faire un grand nombre de schémas, en tenant compte non seulement des propriétés individuelles des liaisons, mais aussi des différentes manières de les disposer dans l'espace les unes par rapport aux autres. L'expérience montre qu'il existe, à ce niveau, une vraie difficulté, en particulier pour un très grand nombre d'étudiants en technologie mécanique et même pour certains de leurs professeurs. C'est pourquoi le lecteur est invité à suivre ce paragraphe, volontairement non illustré, en essayant de ne rien dessiner.
Un petit exemple
On veut lier complètement deux pièces, de façon isostatique, à l'aide d'une liaison composée de deux liaisons simples.
Parmi toutes les solutions permettant d'obtenir le total de 6 degrés de liaison, qui doit être nécessaire et suffisant, la combinaison 3 + 3 est a priori séduisante ; elle conduit à utiliser deux rotules, ou deux appuis plans, ou une rotule et un appui plan. Or, on comprend vite qu'aucune de ces solutions ne convient : quelle que soit la disposition des éléments, il reste toujours au moins un degré de mobilité ET un degré d'hyperstaticité ; dans deux des trois cas (lesquels ?), on peut trouver des dispositions particulières faisant apparaître trois degrés de mobilité ET trois degrés d'hyperstaticité.
Une autre combinaison est 4 + 2, a priori intéressante car elle fait intervenir un pivot glissant, la liaison la moins coûteuse, associé à un appui linéaire rectiligne ou annulaire. Nous laissons au lecteur le soin d'examiner le cas « pivot glissant + linéaire rectiligne », qui ne manque pas d'intérêt, nous réservant d'examiner ci-dessous ce que peut donner une liaison composée d'un pivot glissant et d'une liaison linéaire annulaire.
L'une des pièces comporte une partie sphérique et un cylindre plein ou creux, l'autre un cylindre creux recevant la sphère et un deuxième cylindre creux ou plein ; il devrait être relativement facile de comprendre que les deux possibilités qui sont offertes sont rigoureusement équivalentes et il n'est pas mauvais à ce stade de revenir à la notion de références centrées :
- pour le pivot glissant, il s'agit de l'axe des deux cylindres,
- pour la liaison linéaire annulaire, c'est l'axe du cylindre et le centre de la sphère, le second étant nécessairement situé sur le premier.
On trouvera donc,
- sur l'une des pièces (A par exemple), les axes des deux cylindres ; ceux-ci occuperont a priori une position relative quelconque, que l'on caractérisera par leur distance a, comptée selon leur perpendiculaire commune, et leur angle α,
- sur l'autre pièce (B par exemple), un axe et un point ; a priori la distance b du point à l'axe n'est pas nulle, ce qui correspond à la position la plus probable où le point n'est pas situé sur l'axe.
Sans faire appel à de lourdes démonstrations mathématiques, le lecteur vérifiera :
- facilement, que si b < a le montage est impossible,
- et sans doute un peu plus difficilement que si b > a, lorsque l'assemblage est possible (dans quel cas ne l'est-il pas ?), la liaison est complète et donc forcément isostatique.
Reste le cas fort intéressant où b = a.
Que ces deux distances soient nulles ou non, le centre de la sphère est obligatoirement sur la perpendiculaire commune aux deux axes et la force transmise dans la direction de cette perpendiculaire commune ne peut plus être déterminée, il y a donc au moins un degré d'hyperstaticité.
- si b = a ≠ 0 :
- dans le cas le plus général où α ≠ 0, les liaisons ne permettent pas à l'une des pièces d'empêcher un mouvement hélicoïdal de l'autre, mais ce mouvement s'arrête dès qu'il a commencé, du moins dans le cadre de nos hypothèses : ni jeu ni serrage, solides parfaits. On a donc une glissière hélicoïdale hyperstatique de degré 1 vite transformée en « machine à coincer ».
- si les axes sont orthogonaux (on dit bien orthogonaux et pas perpendiculaires), la translation est supprimée et la liaison composée se transforme en pivot, toujours hyperstatique de degré 1, et toujours de type « machine à coincer ».
- si les axes sont parallèles, alors la rotation est interdite et seule demeure la translation. Nous avons une glissière, toujours hyperstatique de degré 1, mais qui n'est plus vraiment une « machine à coincer » car elle permet un mouvement de grande amplitude. Il n'empêche qu'il existe des solutions sans doute plus géniales pour fabriquer des glissières, celle-ci aura toutes les chances de mal fonctionner, malgré les deux miracles qui devront être faits à l'atelier pour réaliser la condition a = b et le parallélisme absolu des axes.
- si b = a = 0 :
- lorsque les axes des deux liaisons ne sont pas alignés (on dit bien alignés, et non plus simplement parallèles), toute translation est interdite et la liaison devient un pivot hyperstatique de degré 1, qui ne constituera pas l'avancée technologie du siècle si on essaie de le réaliser ; le fait que les axes puissent être perpendiculaires (on dit bien perpendiculaires et non orthogonaux) ne constitue plus un cas particulier.
- lorsque les deux axes des liaisons sont alignés, alors la liaison composée devient un pivot glissant hyperstatique d'ordre 2. On a « gagné » un degré de mobilité ET un degré d'hyperstaticité.
Il est impossible de trouver une disposition permettant d'obtenir trois degrés de mobilité, puisque la simple présence du pivot glissant n'en autorise que deux ; les choses en restent donc là. Tout ceci, bien entendu, se démontre mathématiquement, mais tel n'est pas ici notre propos.
Particularités des schémas de mécanismes
La représentation schématique d'un mécanisme est fondamentalement différente de celle d'un circuit hydraulique ou électrique. Sur le papier, peu importe où l'on placera le graphisme conventionnel représentant une pompe, un distributeur, une pile, une résistance, etc. Dans la réalité, d'ailleurs, les éléments hydrauliques peuvent être reliés par des tuyaux souples et pour les éléments électriques, en général, la forme des fils qui les relient importe peu. Il n'en est évidemment pas de même en mécanique, où l'on ne peut représenter valablement les choses qu'en tenant compte de façon rigoureuse de la disposition spatiale des divers éléments.
Il faut parfois même exécuter plusieurs schémas : il arrive en effet que certains mécanismes fonctionnent en général « convenablement », sauf lorsque leurs éléments se trouvent dans des positions particulières pour lesquelles on voit apparaître, en même temps, un même nombre de degrés de mobilité ET d'hyperstaticité. Dans la réalité, cela peut avoir pour conséquence l'apparition de « points durs » ou une défaillance complète.
Il existe une norme indiquant la façon dont les liaisons doivent être représentées schématiquement. L'auteur de ces lignes a eu l'occasion, peu après sa publication, de s'entretenir longuement avec les créateurs de cette norme et d'en souligner certaines insuffisances.
La fonction d'un schéma n'est pas d'être conforme à une norme, mais de permettre ou de faciliter la compréhension d'un mécanisme, d'un processus, du fonctionnement d'un logiciel, d'un cycle biologique ou météorologique, de l'organigramme d'une entreprise, etc.
Bien souvent, le mécanicien inexpérimenté a tendance à fausser une représentation pour pouvoir dessiner les liaisons de façon « conforme ». C'est notamment le cas lorsque des liaisons sont matériellement contenues à l'intérieur d'autres liaisons ; la représentation normalisée se révèle alors tout à fait inadaptée et il faut faire appel à d'autres méthodes qui se rapprochent davantage du dessin technique. Plutôt que de schémas, il vaut alors mieux parler de « dessins simplifiés » ; on les exécute sans jamais perdre de vue le but de son travail, et après une analyse méthodique des paramètres géométriques qui caractérisent le mécanisme à représenter (parallélismes, perpendicularités, angles, distances, intersections, éventuellement proportions et formes, etc.). Une disposition des éléments aussi générale que possible doit être a priori privilégiée ; les situations particulières, s'il en existe, font l'objet de schémas ou de dessins simplifiés complémentaires.
Si tout ce travail peut se faire en entière conformité avec la norme, tant mieux. Sinon, il ne faut pas hésiter à s'affranchir de cette contrainte et à proposer de meilleures solutions, ce qui n'est pas toujours facile ...
Notes et références
- Charles-Pierre Lefebvre Laboulaye, Traité de cinématique, mécanisme appliqué aux machines, au point de vue géométrique, ou Théorie des mécanismes, Paris, L. Mathias, 1849-1854(BNF 30704782) Premier livre titré théorie des mécanismes, référencé à la Bibliothèque nationale de France
- Robert d'Adhémar, ingénieur des arts et manufactures, docteur ès sciences, professeur à l'Institut industriel du nord de la France, Éléments de mécanique à l'usage des ingénieurs. Statique cinématique, Gauthier-Villars,
Voir aussi
Bibliographie
- R. Le Borzec, J. Lotterie, Principes de la théorie des mécanismes, Dunod (1975)