Demi-hypercube (graphe)
Dans la théorie des graphes, une branche des mathématiques, le graphe demi-hypercube [1] est obtenu à partir du graphe hypercube en ne gardant qu'un sommet sur deux et en reliant les sommets qui étaient à une distance de deux. Il est appelé halved cube, halfcube ou demihypercube en anglais[2].
| Demi-hypercube | |
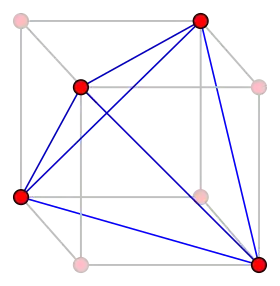 Le graphe demi-hypercube est le graphe tétraédrique | |
| Notation | |
|---|---|
| Nombre de sommets | |
| Nombre d'arêtes | |
| Distribution des degrés | -régulier |
| Automorphismes | |
| Propriétés | Distance-régulier Hamiltonien Symétrique |
Construction
Deux sommets de sont adjacents dans si et seulement s'ils se trouvent exactement à une distance de deux dans . À partir d'un graphe hypercube donné, on peut obtenir deux graphes demi-hypercubes distincts mais isomorphes, suivant le sommet de départ que l'on a choisi.
 |
 |
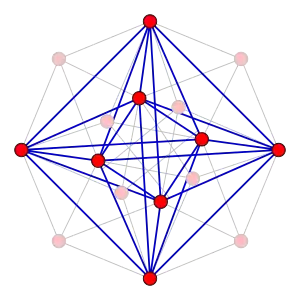
| peut être construit à partir du graphe tesseract en enlevant des sommets. |
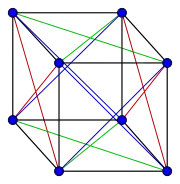
peut aussi être construit à partir du graphe hexaédrique en ajoutant des arêtes. |
On peut aussi obtenir à partir de l'hypercube de dimension inférieure en ajoutant des arêtes entre les sommets à distance deux[1].
Le graphe est le graphe des arêtes et des sommets d'un objet géométrique, le demi-hypercube de dimension .
On peut aussi interpréter comme le graphe de la relation entre les nombres binaires de longueur comportant un nombre pair de 1 (comme 0, 3, 5, 6, 9, etc.[3]) qui sont à une distance de Hamming égale à deux[4].
Exemples
| graphe | sommets | arêtes | degré | illustration | |
|---|---|---|---|---|---|
| 1 | Graphe singleton | 1 | 0 | 0 |  |
| 2 | Graphe chaîne | 2 | 1 | 1 |  |
| 3 | Graphe tétraédrique | 4 | 6 | 3 |  |
| 4 | Graphe de l'hexadécachore | 8 | 24 | 6 |  |
| 5 | Complémentaire du graphe de Clebsch dans le graphe tesseract | 16 | 80 | 10 |
Propriétés
Comme c'est la moitié bipartie d'un graphe distance-régulier, le graphe demi-hypercube est lui-même distance-régulier[5].
Comme c'est la moitié bipartie d'un graphe hamiltonien, il est lui-même hamiltonien.
Notes et références
- (en) C. Godsil, Interesting Graphs and Their Colourings, Manuscrit non publié, , 66 et 67 p. (lire en ligne)
- (en) A hypercube related graph sur MathOverflow
- C'est la suite A001969 de l'OEIS, surnommée par les anglophones evil numbers sequence (suite des « nombres méchants »)
- (en) Piotr Indyk et Jiří Matoušek, « Low-distortion embeddings of finite metric spaces », dans Handbook of Discrete and Computational Geometry, CRC Press, (ISBN 9781420035315, lire en ligne), p. 179.
- (en) Chihara Laura et Dennis Stanton, « Association schemes and quadratic ransformations for orthogonal polynomials », Graphs and Combinatorics, vol. 2, no 2, , p. 101 à 112 (DOI 10.1007/BF01788084, Math Reviews 932118).
Lien externe
(en) Eric W. Weisstein, « Halved Cube Graph », sur MathWorld