Diffusion ambipolaire

La loi de Stefan-Maxwell donne un système d'équations auquel satisfont les flux de diffusion des espèces, chargées ou non, dans un fluide. On simplifie ce système en considérant :

• que les termes liés aux gradients de température et de pression sont négligeables,
• que la charge totale dans le milieu est nulle,

alors:

${\displaystyle \sum _{j\neq i}{\frac {x_{i}x_{j}}{\rho {\mathcal {D}}_{ij}}}\left({\frac {\mathbf {J} _{j}}{c_{j}}}-{\frac {\mathbf {J} _{i}}{c_{i}}}\right)=\nabla x_{i}+{\frac {1}{p}}Q_{i}\mathbf {E} }$

avec

• ${\displaystyle \mathbf {J} _{i}}$ est le flux massique de diffusion pour l'espèce i,
• ${\displaystyle x_{i}}$ la fraction molaire ou volumique,
• ${\displaystyle c_{i}}$ la fraction massique,
• ${\displaystyle {\mathcal {D}}_{ij}}$ le coefficient de diffusion binaire,
• ${\displaystyle \rho =\sum _{i}\rho _{i}}$ la masse volumique,
• ${\displaystyle \rho _{i}=n_{i}m_{i}}$ où ${\displaystyle n_{i}}$ est la densité volumique de particules et ${\displaystyle m_{i}}$ leur masse,
• ${\displaystyle p}$ la pression,
• ${\displaystyle Q_{i}=n_{i}Z_{i}q_{e}}$ la densité de charge pour l'espèce i,
• ${\displaystyle Z_{i}}$ le nombre de charges de la particule i, ${\displaystyle Z_{i}=-1}$ pour l'électron,
• ${\displaystyle q_{e}}$ la charge de l'électron,
• ${\displaystyle \mathbf {E} }$ le champ électrique.

On suppose l'absence de charge globale ${\displaystyle \sum _{i}x_{i}Q_{i}=0}$, ce qui entraîne l'absence de courant électrique :

${\displaystyle \sum _{i}\mathbf {J} _{i}Q_{i}=0}$

On a donc à résoudre en général un système algébrique comportant un nombre d'équations égal au nombre d'espèces N présentes dans le milieu, en effet le système de Stefan-Maxwell est de rang N-1 puisque par définition de la diffusion ${\displaystyle \sum _{i}\mathbf {J} _{i}=0}$.

Rapport ${\displaystyle D_{A}/D_{I}}$ en fonction de la fraction volumique électronique.

Diverses approximations[1] permettent d'écrire le système de Stefan-Maxwell sous forme explicite :

${\displaystyle \mathbf {J} _{i}\simeq -\rho _{i}D_{i}\left(\nabla x_{i}+{\frac {1}{p}}Q_{i}\mathbf {E} \right)}$

où ${\displaystyle D_{i}={\frac {1-w_{i}}{\sum _{k\neq i}{\frac {x_{k}}{{\mathcal {D}}_{ik}}}}}}$

${\displaystyle w_{i}}$ est une pondération que l'on peut prendre égale à ${\displaystyle x_{i}}$ ou ${\displaystyle c_{i}}$[N 1].

Associée à la loi de courant nul, cette équation permet de calculer le champ électrique :

${\displaystyle \mathbf {E} \simeq {\frac {p}{\sum _{i}{\mathcal {D}}_{i}Q_{i}^{2}}}\sum _{i}{\mathcal {D}}_{i}Q_{i}\nabla x_{i}}$

Une analyse asymptotique[2] permet de montrer que les termes liés à l'électron sont dominants dans l'équation ci-dessus et que l'on peut donc l'approximer par :

${\displaystyle \mathbf {E} \simeq {\frac {p}{Q_{e}}}\nabla x_{e}}$

Dans le cas d'un milieu ternaire comprenant un neutre (indice N), un ion (indice I) et des électrons la résolution mène à l'approximation classique :

${\displaystyle \mathbf {J} _{N}\simeq -\rho _{N}D_{N}\nabla x_{N}}$

${\displaystyle \mathbf {J} _{I}\simeq -\rho _{I}D_{A}\nabla x_{I}}$

${\displaystyle \mathbf {J} _{e}\simeq 0}$

avec ${\displaystyle D_{A}=2D_{I}}$ où ${\displaystyle D_{I}}$ est le coefficient de diffusion calculé en l'absence de champ électrique.

Le flux ionique est doublé et le flux électronique nul.

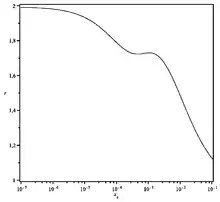
L'approximation pour le flux ionique n'est valable que pour des densités électroniques très faibles (voir courbe).

• Portail de la physique