Divergence de Bregman
En mathématiques, la divergence de Bregman est une mesure de la différence entre deux distributions dérivée d'une fonction potentiel U à valeurs réelles strictement convexe et continûment différentiable.
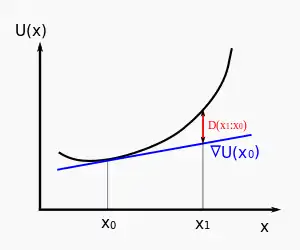
Le concept a été introduit par Lev M. Bregman (en) en 1967[1]. Par l'intermédiaire de la transformation de Legendre, au potentiel correspond un potentiel dual et leur différentiation donne naissance à deux systèmes de coordonnées duaux.
Définition
Soit une fonction à valeurs réelles, strictement convexe et continûment différentiable définie sur un domaine convexe fermé . La divergence de Bregman d'un point de par rapport à un autre point de est :
Propriétés
La divergence de Bregman possède certaines des propriétés d'une distance :
- Positivité : .
- Séparation : .
Par contre, la symétrie et l'inégalité triangulaire ne sont pas vérifiées, ce qui fait qu'elle n'est pas une distance.
Autres propriétés :
- Convexité : la divergence est convexe par rapport à son premier argument.
- Linéarité : pour deux fonctions convexes U et V à valeur réelle et un réel .
- Dualité : la divergence de Bregman est de nature duale[2] : par transformation de Legendre de , on obtient une fonction dont la divergence associée est symétrique par rapport à :
- .
Les points x et y étant exprimés selon deux systèmes de coordonnées duaux issus de la transformation de Legendre : et . La divergence peut être réécrite sous la forme :
- .
Exemples
- La distance de Mahalanobis (et donc la distance euclidienne) sont des divergences de Bregman auto-duales :
- ,
avec
- .
- les α-divergences popularisées par Amari[3] sont un autre exemple.
La divergence entre une distribution p par rapport à une distribution q est définie par :
- .
La divergence duale de est .
Par ailleurs, les α-divergences dérivent des fonctions potentiels :
et des coordonnées associées :
- .
On a alors la relation de dualité des transformées de Legendre :
- .
Par ailleurs, avec les notations introduite, la divergence peut être écrite selon sa forme canonique :
- .
Un cas particulier de α-divergence est la divergence de Kullback-Leibler
- La distance de Itakura-Sato :
- ,
avec
- .
Références
- L. Bregman, The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming, USSR Computational Mathematics and Mathematical Physics, Vol. 7(3): 200--217, 1967.
- S. Amari, Information geometry in optimization, machine learning and statistical inference, Front. Electr. Electron. Eng. China, vol. 5(3), pp. 241-260, 2010, DOI 10.1007/s11460-010-0101-3
- S. Amari, H. Nagaoka, Methods of information geometry, Translations of mathematical monographs; v. 191, American Mathematical Society, 2000 (ISBN 978-0821805312)
- Portail des mathématiques