Problème du stable maximum
En informatique théorique, le problème du stable maximum ou maximum independent set problem en anglais, est un problème d'optimisation qui consiste étant donné un graphe non orienté à trouver un stable de cardinal maximum, c'est-à-dire un sous-ensemble de sommets du graphe, le plus grand possible, tel que les éléments de ce sous-ensemble ne soient pas voisins.
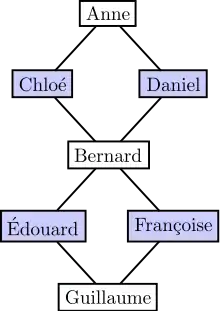
Exemple
Prenons l'exemple du graphe donné à droite. Il représente l'organisation d'un dîner[1] où les invités potentiels sont Anne, Bernard, Chloé, Daniel, Édouard, Françoise et Guillaume. Les sommets sont les invités potentiels. Mais Anne et Chloé ne s'apprécient pas, Anne et Daniel ne s'apprécient pas, Chloé et Bernard ne s'apprécient pas, etc. Il y a une arête entre deux personnes qui ne s'apprécient pas. L'objectif est d'inviter le maximum de personnes qui s'apprécient mutuellement. Il s'agit donc de trouver un stable maximum.
Résolution exacte
Complexité
Le problème de décision associé au problème du stable maximum est le suivant : étant donné un graphe G et un entier k, décider si un stable de taille supérieure à k existe dans un graphe G. Le problème de décision associé au problème du stable maximum et le problème de décision associé au problème de la clique maximale sont interréductibles : il existe un stable de taille supérieure à k dans un graphe G si et seulement si il existe une clique de taille supérieure à k dans le graphe complémentaire de G (obtenu en retirant les arêtes présentes dans le graphe d'origine et en ajoutant les arêtes absentes dans le graphe d'origine). Ainsi, le problème de décision associé au problème du stable maximum est NP-complet au sens de la théorie de la complexité, comme le problème de la clique maximum, et fait partie des 21 problèmes NP-complets de Karp[2],[3].
Problème restreint à certaines classes de graphes
On peut étudier le problème du stable maximum sur des classes de graphe particulière. Par exemple le problème peut être résolu en temps linéaire sur les graphes cordaux[4] mais reste NP-complet sur les graphe de boxicité (en) 2 (i.e les graphes représentant des intersections de rectangles dans le plan, alignés selon les axes)[5].
Approximation
Le problème est aussi difficile à approximer. Pour tout , il est NP-difficile d'approximer la taille du stable maximum avec un ratio [6]. En particulier, si P est différent de NP le problème n'est pas dans la classe APX.
Problèmes proches
Le problème est équivalent au problème de la clique maximum, puisqu'un stable est une clique dans le graphe complémentaire. Ainsi ces deux problèmes ont la même complexité. Cependant quand on réduit l'ensemble des graphes d'entrée (par exemple on cherche un stable maximum pour des graphes cordaux), cette équivalence n'est plus aussi pertinente puisque le graphe complémentaire peut ne pas appartenir à la classe.
- Le problème de couverture par sommets (i.e. le problème du transversal) : Il s'agit de déterminer un transversal minimum. L'équivalence vient du fait que le complémentaire d'un transversal de G (par rapport à l'ensemble X) est un stable de G. Attention ce problème n'est pas équivalent au sens de l'approximation[réf. souhaitée].
Les problèmes suivants ne nécessitent qu'une simple transformation pour être reformulés comme un problème de stable maximum:
- Problème de la maximisation d'une fonction pseudo booléenne (par exemple la fonction ). L'équivalence passe par la construction d'un graphe auxiliaire. Associons à chaque monôme de la fonction un sommet du graphe, auquel on donne un poids égal au coefficient du monôme. Relions deux sommets par une arête lorsque le produit booléen des deux monômes correspondants est nul. Ainsi le maximum de la fonction est égal au poids maximum d'un stable du graphe. Avec la fonction f donnée en exemple, on obtient le graphe suivant :
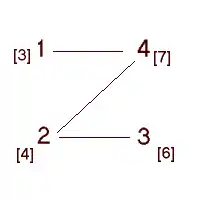
- Ici le stable maximum est composé des sommets 3 et 4 et a pour poids 13, le maximum de f vaut 13 (il est atteint par , c'est-à-dire lorsque seuls les troisième et quatrième monômes valent 1. Il existe une variante pondérée du problème du stable maximum où chaque sommet possède un poids et le but est de trouver un stable de poids maximal.
Notes et références
- (en) « Complexity theory à la Technische Üniverstät München », p. 23
- Sous le nom CLIQUE.
- (Karp 1972)
- (Rose, Tarjan et Lueker 1976)
- (Fulkerson et Gross 1965)
- David Zuckerman, « Linear Degree Extractors and the Inapproximability of Max Clique and Chromatic Number », Theory of Computing, vol. 3, no 1, , p. 103-128
Bibliographie
- (en) Richard M. Karp, « Reducibility Among Combinatorial Problems », dans Raymond E. Miller et James W. Thatcher, Complexity of Computer Computations, Plenum, (ISBN 978-1-4684-2003-6, DOI 10.1007/978-1-4684-2001-2_9, lire en ligne), p. 85-103
- (en) Donald J. Rose, R.Endre Tarjan et George S. Lueker, « Algorithmic aspects of vertex elimination on graphs. », SIAM Journal on Computing, vol. 5, , p. 266-283 (ISSN 0097-5397 et 1095-7111, DOI 10.1137/0205021)
- Delbert R Fulkerson et Oliver A Gross, « Incidence matrices and interval graphs », Pacific J. Math, vol. 15, no 3,
- B Ambert et P Castéra, Réalisation d'un algorithme efficace pour la détermination en ensemble stable de poids maximal d'un graphe, Mémoire d'ingénieur de l'Institut d'Informatique d'Entreprise (IIE-CNAM), Paris 1981
- Portail de l'informatique théorique