Enstrophie

L'enstrophie est définie comme la variance de la vorticité. Cette quantité joue un rôle important en turbulence bidimensionnelle, laquelle constitue une approximation de phénomènes fondamentaux en physique de l'atmosphère où le rapport des échelles caractéristiques (dimension géographique sur altitude) est de l'ordre de 100, ou pour les plasmas magnétisés.

Le phénomène turbulent en deux dimensions d'espace possède des caractères radicalement différents de la cascade d'énergie turbulente tridimensionnelle. On le caractérise par une double cascade d'énergie et d'enstrophie.

Définitions

Pour un écoulement incompressible la vorticité (ou tourbillon) est définie comme le rotationnel de la vitesse V ou parfois la moitié de cette valeur. En géométrie plane (x, y)

{\boldsymbol {\Omega }}=\nabla \times \mathbf {V} =(0,0,\Omega )^{t}\,,\qquad \Omega ={\frac {\partial V_{y}}{\partial x}}-{\frac {\partial V_{x}}{\partial y}}

Pour toute quantité g, notons ${\overline {g}}$ la moyenne statistique de g. On suppose le milieu homogène et stationnaire en moyenne : ${\overline {V}}(x,y,t)=C^{ste}$ . La moyenne statistique se ramène donc à une moyenne temporelle.

Dans un milieu turbulent on décompose

la vitesse en moyenne temporelle et fluctuation v

\mathbf {V} ={\overline {\mathbf {V} }}+\mathbf {v}

la vorticité en moyenne temporelle et fluctuation ω

\Omega ={\overline {\Omega }}+\omega

On définit alors

l'énergie $k={\frac {1}{2}}\langle v^{2}\rangle$
l'enstrophie ${\mathcal {E}}={\frac {1}{2}}\langle \omega ^{2}\rangle$

La turbulence peut être décrite comme un processus stochastique portant sur v ou ω où on associe un nombre d'onde κ à chaque échelle caractéristique. Le processus est caractérisé par une densité d'énergie E (κ) qui permet d'exprimer l'énergie cinétique turbulente k, la dissipation d'énergie ε et l'enstrophie

k=\int _{0}^{\infty }E(\kappa )\mathrm {d} \kappa \,,\qquad \epsilon =2\nu \int _{0}^{\infty }\kappa ^{2}E(\kappa )\mathrm {d} \kappa \,,\qquad {\mathcal {E}}=\int _{0}^{\infty }\kappa ^{2}E(\kappa )\mathrm {d} \kappa

Propriétés

Conservation

La conservation de la vorticité pour un fluide incompressible barotrope est donnée par l'équation de Helmholtz. Dans le problème bidimensionnel on vérifie

({\boldsymbol {\Omega }}\cdot \nabla )\mathbf {V} \equiv 0

d'où l'équation de conservation du tourbillon en bidimensionnel

{\frac {D{\boldsymbol {\Omega }}}{Dt}}={\frac {\partial {\boldsymbol {\Omega }}}{\partial t}}+(\mathbf {V} \cdot \nabla ){\boldsymbol {\Omega }}=\nu \nabla ^{2}{\boldsymbol {\Omega }}

Le système vérifie[1]^,[2]

{\frac {DE}{Dt}}=-\nu {\mathcal {E}}\,,\qquad {\frac {D{\mathcal {E}}}{Dt}}=-\nu \langle (\nabla \omega )^{2}\rangle =-\zeta

Dans un milieu sans viscosité, l'énergie est conservée, pas l'enstrophie.

Cascade enstrophique

Cascade enstrophique.

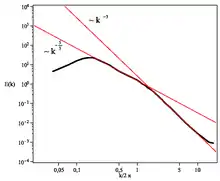
Dans la turbulence bidimensionnelle l'absence de possibilité de l'étirement tourbillonnaire, phénomène fondamental de la turbulence tridimensionnelle[3], change totalement la phénoménologie.

Robert Kraichnan[4], Cecil Leith[5] et George Batchelor[6] ont établi par analyse dimensionnelle un mécanisme analogue à la cascade turbulente concernant l'évolution d'un système homogène et stationnaire lorsque l'on injecte de l'énergie au nombre d'onde κ_F, conduisant à un spectre auto-similaire :

pour κ_F < κ < κ_η le spectre d'énergie pour le transfert des grandes longueurs d'onde vers les plus petites est donné par

E(\kappa )\simeq k^{-3}\zeta ^{\frac {2}{3}}

la dissipation se fait à l'échelle κ_η valeur analogue à la dimension de Kolmogorov

\kappa _{\eta }=\zeta ^{\frac {1}{6}}\nu ^{-3}

pour κ_L < κ < κ_F il peut exister une cascade inverse (des petites vers les grandes longueurs d'onde) d'énergie qui correspond au spectre de Kolmogorov (ou spectre inertiel)

E(\kappa )\simeq \epsilon ^{\frac {2}{3}}k^{-{\frac {5}{3}}}

L'énergie va vers les grandes échelles : il faut donc qu'existe un mécanisme de dissipation de celles-ci. D'une façon générale ce mécanisme entraîne la création de grandes structures cohérentes qui n'ont pas leur équivalent en turbulence tridimensionnelle[1].

Une autre différence notable avec le problème tridimensionnel est l'absence d'intermittence.

Notes et références

(en) Christophe Bailly et Geneviève Compte-Bellot, Turbulence, Springer, 2015 (ISBN 978-3-319-16159-4)
(en) Marcel Lesieur, Turbulence in Fluids, Kluwer Academic Publishers, 1997 (ISBN 0-7923-4415-4)
Étienne Guyon, Jean-Pierre Hulin et Luc Petit, Hydrodynamique physique, CNRS Éditions/EDP Sciences, 2001 (ISBN 2-86883-502-3)
(en) Robert H. Kraichnan, « Inertial Ranges in Two-Dimensional Turbulence », Physics of Fluids, vol. 10, n^o 7,‎ 1967, p. 1417-1423
(en) C. E. Leith, « Diffusion Approximation for Turbulent Scalar Fields », Physics of Fluids, vol. 11, n^o 8,‎ 1968, p. 1612
(en) G. K. Batchelor, « Computation of the Energy Spectrum in Homogeneous Two-Dimensional Turbulence », Physics of Fluids, vol. 12, n^o 12,‎ 1969, p. 233-239

Voir aussi

Portail de la physique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[Bailly-1] (en) Christophe Bailly et Geneviève Compte-Bellot, Turbulence, Springer, 2015 (ISBN 978-3-319-16159-4)

[2] (en) Marcel Lesieur, Turbulence in Fluids, Kluwer Academic Publishers, 1997 (ISBN 0-7923-4415-4)

[Guyon-3] Étienne Guyon, Jean-Pierre Hulin et Luc Petit, Hydrodynamique physique, CNRS Éditions/EDP Sciences, 2001 (ISBN 2-86883-502-3)

[4] (en) Robert H. Kraichnan, « Inertial Ranges in Two-Dimensional Turbulence », Physics of Fluids, vol. 10, n^o 7,‎ 1967, p. 1417-1423

[5] (en) C. E. Leith, « Diffusion Approximation for Turbulent Scalar Fields », Physics of Fluids, vol. 11, n^o 8,‎ 1968, p. 1612

[6] (en) G. K. Batchelor, « Computation of the Energy Spectrum in Homogeneous Two-Dimensional Turbulence », Physics of Fluids, vol. 12, n^o 12,‎ 1969, p. 233-239