Expansion de Shannon
L'expansion de Shannon est, en logique, la décomposition d'une équation booléenne selon une ou plusieurs variables principales. Elle consiste en l'identité suivante, vraie quelle que soit la fonction : où est une formule booléenne, est une variable, est la négation de , et les formules et sont obtenus à partir de en affectant à et respectivement[1].
Pour les articles homonymes, voir Shannon.
Application
Le thèorème d'expansion de Shannon s'applique en décomposant une équation en membres, étant le nombre de variables principales. On aura ainsi 2 membres lorsque l'on choisit une seule variable principale, 4 pour deux variables principales, etc.
Par exemple, pour la fonction de 3 variables , si l'on choisit comme variable principale, le théorème d'expansion de Shannon donne l'égalité suivante :
En prenant et comme variables principales, on obtiendra l'égalité suivante :
Utilisation
Le théorème d'expansion de Shannon permet de séparer des variables que l'on considèrera principales, les autres étant des variables secondaires ou introduites. Il permet notamment de faire correspondre une équation avec les entrées d'un multiplexeur. En effet, une fois l'équation décomposée sous la forme de Shannon, il est possible de réaliser l'identité des variables principales avec les termes produits d'une table de vérité. Ainsi, dans l'exemple suivant :
Le terme produit est associé à , le terme est associé à , etc. On peut donc construire la table de vérité suivante :
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Cette table peut alors être mise en œuvre en utilisant un multiplexeur de la manière suivante :
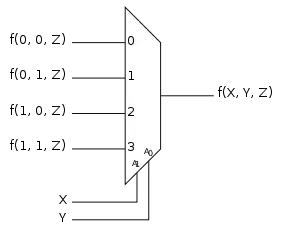
Notes et références
- C. E. Shannon, « The synthesis of two-terminal switching circuits », The Bell System Technical Journal, vol. 28, no 1, , p. 59–98 (ISSN 0005-8580, DOI 10.1002/j.1538-7305.1949.tb03624.x, lire en ligne, consulté le )
- Portail de la logique