Flexagone
Le flexagone est un objet plat de forme polygonale, en général construit par pliage de papier, pouvant par dépliage et repliage suivant les mêmes plis, présenter d'autres faces que les faces initiales. Sa construction s'inspire du ruban de Moebius.
Il en existe plusieurs formes, mais la plus connue est le trihexaflexagone: un hexagone formé de 9 triangles équilatéraux, et qui contient trois faces différentes.
Les préfixes que l’on peut ajouter au nom indiquent le nombre de faces différentes du flexagone puis son nombre de côtés. Par exemple, un hexa-tétra-flexagone a la forme d’un carré et possède six faces différentes, un dodéca-hexa-flexagone a la forme d'un hexagone et possède douze faces différentes, etc.
Histoire
Le flexagone a été découvert par Arthur Harold Stone, un étudiant en mathématiques britannique, en 1939, alors qu’il étudiait à Princeton. Le format de papier aux États-Unis (lettersize) étant différent de celui d'Angleterre (foolscap), il recoupa ses feuilles de cours pour les adapter à son classeur, et joua avec les bandes de papier ainsi obtenues[1].
L’objet enthousiasma plusieurs personnes qui fondèrent un « Comité d'investigation chargé d'enquêter sur les propriétés du flexagone ». Il était composé de plusieurs personnes, qui deviendront ensuite célèbres dans leur disciplines respectives : Bryant Tuckerman, étudiant en mathématiques, Richard P. Feynman, étudiant en physique, et John W. Tukey, alors jeune professeur de mathématiques[1].
B. Tuckerman mit au point une méthode topologique appelée Tuckerman traverse (« déplacement de Tuckerman ») pour révéler toutes les faces d’un flexagone[1].
Les flexagones ont ensuite été introduits au grand public par Martin Gardner, un spécialiste des mathématiques récréatives, qui écrivit à leur propos dans sa rubrique «Mathematical Games» pour le magazine Scientific American[2].
En 1955, Russell Rogers et Leonard D'Andre demandèrent un brevet d’exploitation pour le hexahexaflexagone, qui leur fut accordé en 1959, et qui imaginait l’objet en tant que jouet, ayant une visée publicitaire ou un but éducationnel[3].
Différents flexagones
Le tritétraflexagone
Le tritétraflexagone est le plus simple des tétraflexagones. Il a la forme d’un carré et possède trois faces différentes.
L’hexatétraflexagone cyclique
Il s’agit d’un tétrahexagone possédant six faces, et dont la construction ne requiert pas de colle. Il a la particularité d’être cyclique, c’est-à-dire que l’on ne rencontre pas d’impasse lors de son pliage, mais que l’on retombe indéfiniment sur sa position initiale.
Hexaflexagones
L'objet plat à la forme d'un hexagone. Selon l'épaisseur, il peut correspondre à un trihexaflexagone, un tetrahexaflexagone ou un hexahexaflexagone
Le trihexaflexagone
C'est le plus simple et le plus connu, il est constitué à partir d'une bande de papier pliée en 9 triangles équilatéraux (10 si l’on compte la face servant à coller les bords opposés).
Il peut fléchir (to flex en Anglais) en trois faces différentes.
Patron recto-verso d'un trihexaflexagone. Plier ensuite la partie gauche de la bande vers l'avant selon l'arête R2R3.
Bande après le premier pliage. Plier ensuite la partie droite vers l'arrière selon l'arête R5R6.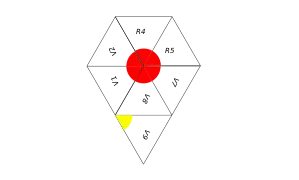
Bande après le second pliage. Rabattre ensuite V9 vers l'arrière et l'ajuster par une arête à R1. La face de devant dessine un cercle rouge, la face de derrière un cercle jaune éclaté.
L’hexahexaflexagone
C’est une forme plus complexe du flexagone, fabriquée à partir d’une bande de papier de 18 triangles équilatéraux. Celle-ci est repliée sur elle-même de façon à avoir la longueur de 9 triangles, puis est ensuite pliée comme un trihexaflexagone.
Il permet d'obtenir 6 groupes de 6 faces différents selon 18 configurations différentes (9 recto et 9 verso) dans des cycles à 12 étapes.
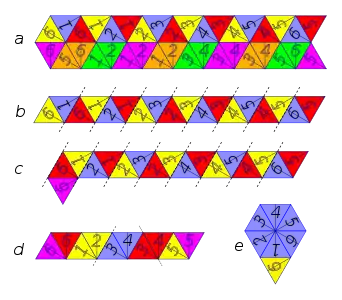Patron et plan de construction d'un hexa-hexa-flexagone:
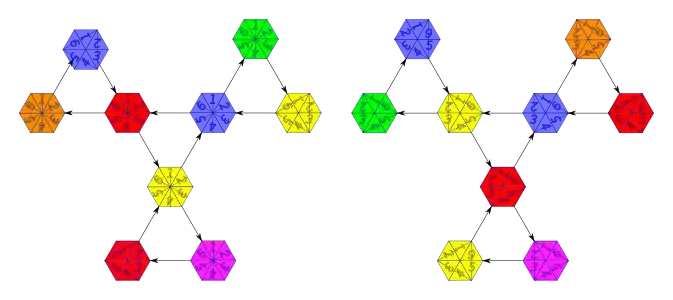
Schémas de pliage (Tuckerman Traverse) recto et verso.
Dans l'illustration ci-dessus, on a:
- a - Patron recto verso (replier selon l'axe de symétrie et coller le recto au verso)
- b - Axes de pliage vers l'arrière
- c - Début de pliage en spirale
- d - Fin du pliage en spirale - Pour finir la réalisation, il faut plier à droite vers l'avant selon 3R-4R et à gauche vers l'arrière selon 2J-3B
- e - Fin de réalisation : il reste à replier 6J vers l'arrière et l'ajuster à 5M)
Bibliographie
- Martin Gardner, Hexaflexagons and Other Mathematical Diversions: The First Scientific American Book of Puzzles and Games, University of Chicago Press, (présentation en ligne)
- Les Pook, Flexagons Inside Out, Cambridge University Press, (présentation en ligne)
Liens externes
- (en) Eric W. Weisstein, « Flexagon », sur MathWorld
- Les hexaflexagones sur la chaîne YouTube Micmaths de Mickaël Launay.
- (en) « The Flexagon Portal », Présentation et patrons de flexagones,
Notes et références
- Martin Gardner, Hexaflexagons and Other Mathematical Diversions: The First Scientific American Book of Puzzles and Games, University of Chicago Press, (présentation en ligne)
- Jürgen Köller, « Flexagons » (consulté le )
- RE Rogers et al., « Patent 2,883,195: Changeable Amusement Devices And The Like », (consulté le )
Portail de la géométrie