Fonction cubique

En mathématiques, une fonction cubique est une fonction de la forme

f(x)=ax^{3}+bx^{2}+cx+d

,

Courbe représentative de la fonction cubique

f (x) = (x 3 + 3 x 2 - 6 x - 8)/4

, qui a 3 racines réelles (où la courbe croise l'axe horizontal — où y = 0) et deux points critiques.

où $a$ est non nul.

L'équation $f (x) = 0$ est alors une équation cubique.

Les solutions de cette équation polynomiale sont appelées zéros de la fonction polynomiale $f$ .

Points critiques

Les racines, les points stationnaires, point d'inflexion et la concavité d'un polynôme cubique

x 3 -3x 2 -144x+432

(ligne noire) et ses dérivées première et seconde (rouge et bleu).

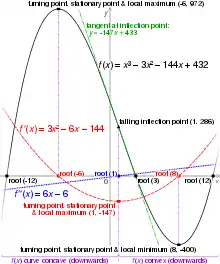
On considère ici une fonction cubique $f$ définie par $f (x) = ax 3 + bx 2 + cx + d$ dont les coefficients, ainsi que la variable $x$ , sont réels.

Les points critiques de $f$ sont les abscisses des points du graphe où la pente de la tangente est nulle, c'est-à-dire les $x$ en lesquels la dérivée de $f$ s'annule :

3ax^{2}+2bx+c=0

.

Les solutions de cette équation sont données, en utilisant la formule quadratique avec discriminant réduit :

x_{\text{critique}}={\frac {-b\pm {\sqrt {\Delta _{0}}}}{3a}}

.

avec

\Delta _{0}=b^{2}-3ac

.

Le signe de $Δ 0$ détermine le nombre de points critiques et d'extrema locaux de $f$ :

si $Δ 0 > 0$ — comme dans le diagramme ci-contre — alors $f$ a un maximum local et un minimum local ;
si $Δ 0 = 0$ , alors le point d'inflexion (cf. ci-dessous) est le seul point critique ;
si $Δ 0 < 0$ , alors $f$ n'a pas de point critique.

Dans les cas où $Δ 0 \leq 0$ , $f$ est strictement monotone donc n'a pas d'extremum local.

La valeur de $Δ 0$ joue également un rôle important dans la détermination de la nature et des valeurs des racines de l'équation cubique.

Point d'inflexion et symétrie

La courbe d'une fonction cubique générale,

f(x)=ax^{3}+bx^{2}+cx+d

,

a toujours un point d'inflexion, c'est-à-dire un point où la courbe change de concavité.

Puisque la dérivée seconde de $f$ s'exprime par $f''(x) = 6 ax + 2 b$ , l'abscisse de ce point est

x_{0}:=-{\frac {b}{3a}}

,

valeur qui est également importante dans la résolution de l'équation cubique.

L'ordonnée est

y_{0}:=f(x_{0})=

2 b 3 / 27 a 2 - bc / 3 a + d

.

La courbe est symétrique par rapport à ce point[1].

Démonstration

En intégrant deux fois $f''(x_{0}+h)=6ah$ , on obtient $f'(x_{0}+h)=3ah^{2}+f'(x_{0})$ , puis $f(x_{0}+h)-y_{0}=ah^{3}+hf'(x_{0})$ , qui est une fonction impaire de $h$ .

Applications

Les fonctions cubiques apparaissent dans divers contextes.

Le théorème de Marden indique que les foyers de l'inellipse de Steiner d'un triangle peuvent être trouvés en utilisant la fonction cubique dont les racines sont les coordonnées dans le plan complexe de trois sommets du triangle. Les racines de la première dérivée de ce cube sont les coordonnées complexes de ces foyers.

Le polynôme caractéristique d'une matrice 3 × 3 est de degré 3.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Cubic function » (voir la liste des auteurs).

(en) Michael de Villiers, « All cubic polynomials are point symmetric », Learning & Teaching Mathematics, vol. 1,‎ 2004, p. 12-15 (lire en ligne).

Voir aussi

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Michael de Villiers, « All cubic polynomials are point symmetric », Learning & Teaching Mathematics, vol. 1,‎ 2004, p. 12-15 (lire en ligne).