Indicatrice de Carmichael
La fonction indicatrice de Carmichael, ou indicateur de Carmichael ou encore fonction de Carmichael, notée λ, est définie sur les entiers naturels strictement positifs ; elle associe à un entier n le plus petit entier m vérifiant, pour tout entier a premier avec n, am ≡ 1 mod n. Elle est introduite par Robert Daniel Carmichael dans un article de 1910.
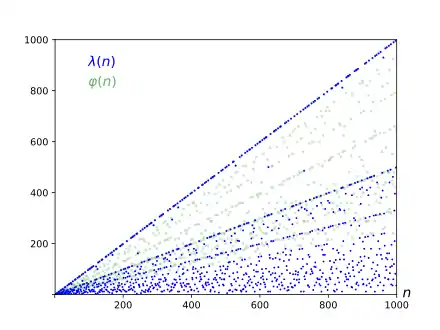
L'indicatrice de Carmichael λ entretient des rapports étroits avec la fonction indicatrice d'Euler φ, en particulier λ(n) divise φ(n). Les deux fonctions coïncident en 1, 2, 4, les puissances d'un nombre premier impair et leurs doubles, mais diffèrent partout ailleurs.
Définitions et première propriétés
Les entiers a premiers avec n sont exactement ceux qui sont inversibles modulo n (par le théorème de Bachet-Bézout et sa réciproque). Donc si deux entiers m et k vérifient am ≡ 1 mod n et ak ≡ 1 mod n, le reste de la division euclidienne de l'un par l'autre également. La définition peut donc être reformulée[1] :
- λ(n) est l'unique entier tel que
- pour tout entier a premier avec n, aλ(n) ≡ 1 mod n
- si pour tout entier a premier avec n, am ≡ 1 mod n, alors λ(n) divise m.
On déduit alors du théorème d'Euler que :
- λ(n) divise φ(n).
La définition a également pour conséquence, par le théorème des restes chinois que :
- si m et n sont premiers entre eux, alors λ(m×n) est le plus petit commun multiple de λ(m) et λ(n).
La définition peut être reformulée en utilisant la théorie des groupes. Un entier a premier avec n est exactement un entier dont la classe modulo n est un élément inversible de l'anneau ℤ/nℤ, c'est-à-dire un élément du groupe multiplicatif (ℤ/nℤ)*. Par définition, le plus petit entier m vérifiant αm = 1 pour tout élément α d'un groupe est appelé exposant de ce groupe, et donc :
- λ(n) est l'exposant du groupe multiplicatif (ℤ/nℤ)* des éléments inversibles de l'anneau ℤ/nℤ.
Une autre caractérisation de l'exposant donne
- λ(n) est le plus petit commun multiple des ordres des éléments de (ℤ/nℤ)*.
On retrouve ainsi que λ(n) divise φ(n) qui est le cardinal, ou ordre, du groupe (ℤ/nℤ)* et donc un multiple commun des ordres de ses éléments (par le théorème de Lagrange).
Dans un groupe commutatif fini, comme (ℤ/nℤ)*, il existe un élément d'ordre l'exposant, c'est-à-dire que :
- il existe un élément de (ℤ/nℤ)* d'ordre λ(n).
On en déduit immédiatement que :
- λ(n) = φ(n) si et seulement si le groupe (ℤ/nℤ)* est un groupe cyclique.
Quand p est premier, ℤ/pℤ est un corps fini (premier), et son groupe multiplicatif (ℤ/pℤ)* est alors cyclique. Donc :
- si p est premier, λ(p) = φ(p) = p - 1.
Exemples
On n'a pas toujours λ(n) = φ(n) : le groupe multiplicatif (ℤ/8ℤ)* est le groupe de Klein, d'ordre 4 et d'exposant 2, on a donc λ(8) = 2 mais φ(8) = 4.
Il n'y a pas que les nombres premiers pour lesquels les fonctions φ et λ prennent la même valeur : on vérifie que (ℤ/4ℤ)* et (ℤ/6ℤ)* sont d'ordre 2, donc λ(4) = φ(4) = 2 et λ(6) = φ(6) = 2, (ℤ/9ℤ)* est d'ordre φ(9) = 6, et 2 est un élément d'ordre 6 de (ℤ/9ℤ)* donc λ(9) = φ(9) = 6 (les cas où φ(n)= λ(n) sont précisés au paragraphe suivant).
La suite oeis:A002322 donne les premières valeurs de la fonction λ de Carmichael (et en propose d'autres dans les références). Les 36 premières valeurs de la fonction λ sont données dans le tableau ci-dessous, avec celles de l'indicatrice d'Euler φ correspondantes.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λ(n) | 1 | 1 | 2 | 2 | 4 | 2 | 6 | 2 | 6 | 4 | 10 | 2 | 12 | 6 | 4 | 4 | 16 | 6 | 18 | 4 | 6 | 10 | 22 | 2 | 20 | 12 | 18 | 6 | 28 | 4 | 30 | 8 | 10 | 16 | 12 | 6 |
| φ(n) | 1 | 1 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | 4 | 10 | 4 | 12 | 6 | 8 | 8 | 16 | 6 | 18 | 8 | 12 | 10 | 22 | 8 | 20 | 12 | 18 | 12 | 28 | 8 | 30 | 16 | 20 | 16 | 24 | 12 |
Calcul de λ(n)
On sait calculer λ(m×n) connaissant λ(m) et λ(n) quand m et n sont premiers entre eux. On pourra donc calculer λ(n) à partir de la décomposition en facteurs premiers de n, si on sait calculer λ(pr) pour p un nombre premier, ce que l'on obtient en étudiant les groupes multiplicatifs correspondant :
- si p est un nombre premier impair, et r ≥ 1 un entier, alors le groupe multiplicatif (ℤ/pr ℤ)* est le groupe cyclique d'ordre φ(pr) = pr - pr - 1 ;
- si r ≥ 2, le groupe multiplicatif (ℤ/2r ℤ)*, est un groupe de cardinal φ(2r) = 2r - 1, produit d'un groupe d'ordre 2 et d'un groupe cyclique d'ordre 2r - 2, soit, si r > 2, un groupe d'exposant λ(2r) = 2r - 2, si r = 2 le groupe est de cardinal et d'exposant 2.
On obtient alors une caractérisation plus calculatoire de la fonction indicatrice de Carmichael (prise d'ailleurs parfois pour définition, en particulier dans l'article original de Carmichael[2]).
Théorème de Carmichael. — La fonction indicatrice de Carmichael est la fonction λ définie sur les entiers strictements positifs par :
- λ(1) = 1 ;
- λ(pr) = φ(pr) = pr - pr - 1, pour p premier impair et r > 0, ou p = 2 et 0 < r ≤ 2 ;
- λ(2r) = 12φ(2r) = 2r - 2, pour r > 2 ;
- λ(p1r1 ... pkrk ) = ppcm(λ(p1r1), ... , λ( pkrk)), où les pi sont des nombres premiers distincts.
La fonction indicatrice de Carmichael prend la même valeur que la fonction indicatrice d'Euler en n si et seulement si le groupe (ℤ/nℤ)* est cyclique, c'est-à-dire si et seulement si :
- n = 1 ;
- n = 2 ou n = 4 ;
- n = pr ou n = 2pr, une puissance non nulle (r > 0) d'un entier premier impair p ou le double d'une telle puissance ;
(la suite oeis:A034380 énumère les premières valeurs du quotient φ(n)λ(n), et propose d'autres données en références).
Autres propriétés
On déduit, soit de la définition, soit de la forme plus explicite donnée par le théorème, que :
- si m divise n, alors λ(m) divise λ(n) ;
en particulier :
- si n est divisible par p premier, alors λ(n) est divisible par p - 1 ;
- si n > 2, alors λ(n) est un nombre pair (conséquence du précédent) ;
- si n est divisible par p2 où p est premier, alors λ(n) est divisible par p.
Quand n est un nombre sans facteur carré, c'est-à-dire que n est le produit de nombres premiers distincts p1, ... , pk :
- λ(p1 ... pk) = ppcm(p1 -1, ... , pk - 1) ;
- pour tout entier a, aλ(n) + 1 ≡ a mod n.
Nombres de Carmichael
Les nombres de Carmichael sont des nombres entiers naturels n qui ne sont pas premiers mais qui vérifient pourtant la conclusion du petit théorème de Fermat, soit :
- pour tout entier a premier avec n, an - 1 ≡ 1 mod n.
Carmichael les étudie dans le même article où il introduit sa fonction indicatrice et donne en particulier cette caractérisation[3], qui suit immédiatement de la définition adoptée plus haut :
- un nombre n qui n'est pas premier est de Carmichael si et seulement si λ(n) divise n - 1.
Par conséquent :
- un nombre de Carmichael est forcément impair, car n - 1 est divisible par λ(n) pair (on a n > 2, et voir section précédente) ;
- un nombre de Carmichael n est premier avec λ(n), donc sans facteur carré (voir section précédente), soit produit de nombres premiers tous distincts.
En tirant parti de ces propriétés, et de l'expression dans ce cas de λ(n) (voir section précédente), la caractérisation de Carmichael devient :
Théorème.— Un entier naturel n qui n'est pas premier est un nombre de Carmichael si et seulement s'il est produit de nombres premiers impairs distincts, soit n = p1 … pk, vérifiant pi - 1 divise n - 1, pour 1 ≤ i ≤ k.
Ce résultat, démontré dans l'article de Carmichaël[4], est parfois appelé théorème de Korselt (voir l'article détaillé nombre de Carmichael).
Notes et références
- Demazure 2008, p. 90.
- Carmichael 1910, p. 232.
- Carmichael 1910, p. 237.
- Carmichael 1910, p. 237-238.
Bibliographie
- (en) R. D. Carmichael, « Note on a new number theory function », Bulletin of the American Mathematical Society, vol. 16, no 5, , p. 232–238 (DOI 10.1090/s0002-9904-1910-01892-9, lire en ligne) ;
- Michel Demazure, Cours d'algèbre : Primalité. Divisibilité. Codes., [détail de l’édition] (p 90-94).
- (en) Hans Riesel, Prime Numbers and Computer Methods for Factorization (second edition), Boston, Birkhäuser, , 464 p. (ISBN 0-8176-3743-5, lire en ligne)
- Arithmétique et théorie des nombres