Dilogarithme
En mathématiques, la fonction de Spence, ou dilogarithme, notée Li2, est un cas particulier de polylogarithme. Deux fonctions spéciales sont appelées fonction de Spence :
- le dilogarithme lui-même :
- ;
- sa réflexion.
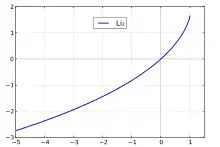
Pour , une définition à l'aide d'une série est également possible (la définition intégrale constituant son prolongement analytique dans le plan complexe) :
- .
William Spence (1777-1815), dont on a donné le nom à cette fonction, est un mathématicien écossais. Il a été condisciple de John Galt, qui a par la suite écrit un essai biographique sur Spence.
Égalités pour des valeurs particulières
Valeurs particulières
En physique des particules
On rencontre couramment la fonction de Spence en physique des particules, dans le calcul des corrections radiatives. Dans ce contexte, la fonction est souvent définie avec une valeur absolue à l'intérieur du logarithme :
Notes et références
- (en) Don Zagier, « The Dilogarithm Function », dans Pierre Cartier, Pierre Moussa, Bernard Julia et Pierre Vanhove (éds.), Frontiers in Number Theory, Physics, and Geometry, vol. II, (ISBN 978-3-540-30308-4, DOI 10.1007/978-3-540-30308-4_1, lire en ligne), p. 3-65.
- (en) Eric W. Weisstein, « Dilogarithm », sur MathWorld.
Voir aussi
Bibliographie
- (en) L. Lewin, Dilogarithms and Associated Functions, Londres, Macdonald,
- (en) Robert Morris, « The dilogarithm function of a real argument », Math. Comp., vol. 33, , p. 778-787 (DOI 10.1090/S0025-5718-1979-0521291-X)
- (en) J. H. Loxton, « Special values of the dilogarithm », Acta Arith., vol. 18, , p. 155-166 (lire en ligne)
- (en) Anatol N. Kirillov, « Dilogarithm identities », Progress of Theoretical Physics Supplement, vol. 118, , p. 61-142 (DOI 10.1143/PTPS.118.61, arXiv hep-th/9408113)
- (en) Carlos Osacar, Jesus Palacian et Manuel Palacios, « Numerical evaluation of the dilogarithm of complex argument », Celest. Mech. Dyn. Astron., vol. 62, , p. 93-98 (DOI 10.1007/BF00692071, Bibcode 1995CeMDA..62...93O)
- (en) Spencer J. Bloch, Higher regulators, algebraic K-theory, and zeta functions of elliptic curves, Providence, RI, AMS, coll. « CRM Monograph Series » (no 11), , 97 p. (ISBN 0-8218-2114-8, zbMATH 0958.19001)
Lien externe
(en) « Dilogarithms », sur NIST Digital Library of Mathematical Functions
- Portail de l'analyse