Fonction quasi-convexe

Une fonction ${\displaystyle f:C\to \mathbb {R} }$ définie sur une partie convexe C d'un espace vectoriel réel E est dite :

• quasi-convexe si pour tout réel ${\displaystyle a}$, l'ensemble de sous-niveau ${\displaystyle \{x\in C\mid f(x)\leq a\}}$ est convexe ou, ce qui est équivalent, si${\displaystyle \forall x,y\in C\quad \forall z\in \left[x,y\right]\quad f(z)\leq \max \left(f(x),f(y)\right)}$ ;
• strictement quasi-convexe si l'on a même :${\displaystyle \forall x,y\in C\quad \forall z\in \left]x,y\right[\quad f(z)<\max \left(f(x),f(y)\right)}$ ;
• quasi-concave si son opposée est quasi-convexe, c'est-à-dire si${\displaystyle \forall x,y\in C\quad \forall z\in \left[x,y\right]\quad f(z)\geq \min \left(f(x),f(y)\right)}$ ;
• strictement quasi-concave si son opposée est strictement quasi-convexe, c'est-à-dire si${\displaystyle \forall x,y\in C\quad \forall z\in \left]x,y\right[\quad f(z)>\min \left(f(x),f(y)\right)}$.
• quasi-linéaire[1]^,[2] (ou quasi-monotone[3]) si elle est à la fois quasi-convexe et quasi-concave.

Toute forme linéaire est quasi-linéaire.

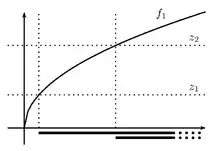
Une fonction monotone est quasi-linéaire, c'est-à-dire à la fois quasi-convexe et quasi-concave.

En plus d'être monotone, cette fonction est strictement concave.

Une fonction ${\displaystyle f}$ définie sur un intervalle ${\displaystyle I\subset \mathbb {R} }$ est quasi-convexe si et seulement si elle est monotone ou « décroissante puis croissante », c'est-à-dire s'il existe dans ${\displaystyle I}$ deux intervalles complémentaires ${\displaystyle I_{1}<I_{2}}$ (l'un des deux pouvant être vide) tels que ${\displaystyle f}$ soit décroissante sur ${\displaystyle I_{1}}$ et croissante sur ${\displaystyle I_{2}}$[4]. De même, ${\displaystyle f}$ est quasi-concave si et seulement si elle est monotone ou « croissante puis décroissante »[5]. Elle est donc quasi-linéaire si et seulement si elle est monotone.

Si une fonction possédant un maximum global en un point m du convexe ${\displaystyle C\subset E}$ est quasi-concave alors elle est unimodale (en), c'est-à-dire croissante le long de tout segment orienté aboutissant en m. La réciproque est vraie si ${\displaystyle E=\mathbb {R} }$ (d'après la caractérisation précédente de la quasi-concavité dans ce cas), mais on construit facilement sur ${\displaystyle \mathbb {R} ^{2}}$ une fonction unimodale et non quasi-concave[6].

En optimisation, les problèmes avec des fonctions objectif quasi-convexes peuvent se résoudre avec les mêmes méthodes que les fonctions objectif convexes. En particulier, dans le cas de problèmes non contraints ou avec un ensemble admissible convexe, tout minimum local est un minimum global, sauf si la fonction est constante au voisinage de ce point[7]. Les algorithmes de descente peuvent être « piégés » par un tel « plateau horizontal ».