Force de Laplace
La force de Laplace est la force électromagnétique qu'exerce un champ magnétique sur un conducteur parcouru par un courant.
Pour les articles homonymes, voir Laplace.
Explication qualitative
Dans un conducteur rectiligne, la force de Laplace est la résultante de toutes les forces de Lorentz sur les charges mobiles. Celles-ci étant bloquées latéralement dans le matériau, cela se traduit par l'existence d'une force latérale sur le conducteur, par le principe d'action-réaction : la force totale se transmet au matériau[1]. Si la force de Lorentz agit sur les particules, la force de Laplace agit sur le matériau conducteur de ces particules[2],[3],[4].
Plus en détail, la circulation d'un courant dans un conducteur s'accompagne d'un mouvement de porteurs de charge. Dans un champ magnétique extérieur, ces particules chargées sont soumises à la partie magnétique de la force de Lorentz :
Les porteurs de charge sont alors temporairement déviés dans le conducteur. L'inhomogénéité des charges dans le conducteur conduit à l'apparition d'un champ de Hall . Ce champ exerce alors une force de Lorentz sur les charges fixes du conducteur (de charge positive) :
Cette force agissant sur la masse du conducteur n'étant pas compensée, le matériau se déplace.
Il ne faut pas confondre la force de Laplace, résultante macroscopique, avec la force de Lorentz, résultante microscopique, sur une particule chargée q en mouvement à une vitesse () dans un champ magnétique.
La différence se situe dans la prise en compte des charges non mobiles présentes dans le matériau (ions du réseau cristallin par exemple) et qui permettent de transmettre la force de Lorentz subie par les charges mobiles à l'ensemble du matériau. Plus précisément, le champ magnétique produit un effet Hall dans le matériau. Il y a donc en plus du champ magnétique, le champ électrique dû à l'effet Hall. Pour les porteurs de charge mobiles du matériau, la force de Lorentz totale est alors nulle (la somme de la partie magnétique et électrique s'annule), alors que les cations, immobiles, du réseau cristallin du matériau ne ressentent que la partie électrique de la force de Lorentz. La résultante macroscopique de cette force est la force de Laplace. La force de Laplace agirait donc par l'intermédiaire de l'effet Hall[5].
Le travail de la composante magnétique de la force de Lorentz est toujours nul, car elle est perpendiculaire au déplacement de l'électron, et seule la composante électrique travaille[6]. Le travail de la force de Laplace n'est pas nul, le matériau se déplaçant dans le sens de la force.
Expression
En utilisant l'expression du champ de Hall, la force exercée sur une charge fixe est :
On note la section du conducteur et la densité volumique de porteurs de charge dans le conducteur. La neutralité électrique assure que est également la densité volumique de charges fixes. La force élémentaire exercée sur un élément de longueur du conducteur est alors :
Or le déplacement des porteurs de charge est colinéaire à l'élément de longueur et la vitesse peut donc s'écrire . La force devient :
Comme la relation entre la vitesse des porteurs de charge et l'intensité du courant électrique est :
L'expression de la force de Laplace est :
On a également dans le cas d'un volume infiniment petit () de particules chargées et avec la densité de courant le traversant :
Rail de Laplace
L'expérience du rail de Laplace (ou des rails de Laplace) illustre la force de Laplace.
Une tige conductrice fermant un circuit placé horizontalement dans un champ magnétique vertical est soumise à la force de Laplace lorsque le courant passe. La tige se met alors en mouvement, et son sens de déplacement est déterminé par la règle de la main droite.
C'est l'expérience fondamentale illustrant le fonctionnement des moteurs électriques.
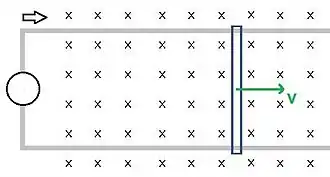
Si est la longueur de la tige, la valeur du champ magnétique, et la valeur du courant, la force de Laplace vaut ici :
Notes et références
- Michel Henry et Abdelhadi Kassiba, Mini manuel d'électromagnétisme, Dunod (2e édition), , 214 p. (ISBN 978-2-10-059125-1, lire en ligne), p. 138
- « Forces de Lorentz et de Laplace » [PDF] (consulté le )
- Julien Calafell, Exos résolus : Prépas Physique-Chimie MPSI, Hachette Education, , 672 p. (ISBN 978-2-01-290667-9 et 2-01-290667-2, lire en ligne), p. 469
- Université de Grenoble, « Actions et énergie magnétique » [PDF], (consulté le ), p. 27
- Harris Benson et Mathieu Lachance (trad. de l'anglais), Physique, vol. 2 : Électricité et magnétisme, Louvain-la-Neuve/Paris, De Boeck, , 5e éd. (1re éd. 1993), 593 p. (ISBN 978-2-8041-9380-5, lire en ligne), chap. 8 (« Le champ magnétique »), p. 342
- Jean-Marie Malherbe, Observatoire de Paris, « Physique I - Éélectromagnétisme, p.2 » [PDF], (consulté le )
Articles connexes
- Portail de la physique
- Portail de l’électricité et de l’électronique