Formulaire de relativité restreinte

Systèmes d'axes parallèles

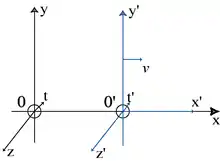
On considère deux référentiels galiléens Oxyz et O’x’y’z’, dont les axes Ox et O’x’ sont confondus, O’y’ et O’z’ étant respectivement parallèles à Ox et Oy. On suppose que le repère O’x’y’z’ se déplace par rapport au repère Oxyz, avec une vitesse constante égale à v le long de l'axe Ox.

Toutes les quantités relatives au premier repère seront notées sans apostrophe (par exemple, un événement y sera localisé par le quadrivecteur${\displaystyle (ct,\mathbf {r} )=(ct,x,y,z)}$), et avec une apostrophe pour le deuxième repère (le quadrivecteur y sera donc noté ${\displaystyle (ct',\mathbf {r'} )=(ct',x',y',z')}$).

On suppose que O et O’ coïncident pour la même origine des temps ${\displaystyle t\,=\,t'\,=\,0}$.

On pose :

${\displaystyle \beta \,=\,{\frac {v}{c}}}$

${\displaystyle \gamma ={\frac {1}{\sqrt {1-\beta ^{2}}}}}$

ou ${\displaystyle \gamma (v)={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$ s'il est nécessaire de préciser la dépendance envers v.

Pour simplifier les formules, il est utile d'introduire le paramètre angulaire de vitesse θ défini par les formules suivantes :

${\displaystyle \beta \,=\,\tanh(\theta )}$   soit   ${\displaystyle \theta \,=\,\mathrm {atanh} (\beta )}$

À l'aide de ce paramètre on peut écrire :

${\displaystyle \gamma ={\frac {1}{\sqrt {1-\tanh ^{2}(\theta )}}}=\cosh(\theta )}$

${\displaystyle \beta \gamma \,=\,\tanh(\theta )\cosh(\theta )=\sinh(\theta )}$

Elles donnent la façon dont se transforme le quadrivecteur ${\displaystyle (ct,\mathbf {r} )}$ de coordonnées spatio-temporelles (ct, x, y, z) d'un même événement quand on passe d'un référentiel à l'autre :

${\displaystyle {\begin{cases}ct=\gamma (ct'+\beta x')\\x=\gamma (x'+\beta ct')\\y=y'\\z=z'\end{cases}}}$

ce qui donne sous forme matricielle (plus facile à visualiser) :

${\displaystyle {\begin{pmatrix}ct\\x\\y\\z\end{pmatrix}}={\begin{pmatrix}\gamma &\beta \gamma &0&0\\\beta \gamma &\gamma &0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}}{\begin{pmatrix}ct'\\x'\\y'\\z'\end{pmatrix}}}$

En utilisant les fonctions hyperboliques de l'angle θ, on obtient des expressions analogues aux formules de changement d'axes de coordonnées par rotation plane, mais avec des fonctions hyperboliques :

${\displaystyle {\begin{cases}ct=ct'\cosh(\theta )+x'\sinh(\theta )\\x=ct'\sinh(\theta )+x'\cosh(\theta )\end{cases}}}$

On obtient les transformations inverses en changeant le signe de la vitesse.

Les transformations de Lorentz s'appliquent à tous les quadrivecteurs.

La quantité suivante est invariante dans un changement de coordonnées

${\displaystyle c^{2}\tau ^{2}\,=\,c^{2}t^{2}-(x^{2}+y^{2}+z^{2})=\,c^{2}t'^{2}-(x'^{2}+y'^{2}+z'^{2})}$

et définit le temps propre ${\displaystyle \,\tau \,.}$

Soit une particule se déplaçant dans le référentiel Oxyz. Si sa position à l'instant t est (x, y, z) et sa vitesse est w, alors on a :

${\displaystyle {\rm {d}}t={\frac {1}{\sqrt {1-{\frac {w^{2}}{c^{2}}}}}}{\rm {d}}\tau =\gamma (w){\rm {d}}\tau }$

Si l'horloge du référentiel O’x’y’z’ mesure la durée ${\displaystyle \Delta \,t'}$ entre deux événements se produisant au même endroit dans ce référentiel, donc séparés par une distance spatiale ${\displaystyle \Delta \,x'=0}$, alors la durée mesurée dans le référentiel Oxyz est :

${\displaystyle \Delta t=\Delta t'\cosh(\theta )=\gamma \Delta t'={\frac {\Delta t'}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,.}$

En particulier, la durée mesurée dans un repère extérieur est toujours plus grande que la durée propre.

Si un objet fixe dans le référentiel O’x’y’z’ est de longueur L’ selon l'axe O’x’ dans ce repère (longueur propre), sa longueur L mesurée au même instant t dans le référentiel Oxyz par la distance entre les deux points de l'axe Ox délimitant l'avant et l'arrière de l'objet, donc correspondant à ${\displaystyle \Delta t\,=\,0}$, est donnée par :

${\displaystyle L={\frac {L'}{\gamma }}=L'{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

La longueur mesurée dans un référentiel par rapport auquel un objet se déplace est plus petite que la longueur propre de l'objet.

Si un point est mobile dans le référentiel O’x’y’z’ avec une vitesse ${\displaystyle \mathbf {w'} }$ parallèle à O’x’ et de module w’ , alors sa vitesse ${\displaystyle \mathbf {w} }$ dans le référentiel Oxyz est parallèle à Ox et son module vaut :

${\displaystyle w\,=\,{\frac {w'+v}{1+{\frac {w'v}{c^{2}}}}}}$

En utilisant les paramètres angulaires,

${\displaystyle \alpha '\,=\,\mathrm {atanh} \left({\frac {w'}{c}}\right)}$

${\displaystyle \alpha \,=\,\mathrm {atanh} \left({\frac {w}{c}}\right)}$

${\displaystyle \theta \,=\,\mathrm {atanh} \left({\frac {v}{c}}\right)}$

on a la loi additive ${\displaystyle \alpha \,=\,\alpha '+\theta }$.

Plus généralement, si la vitesse ${\displaystyle \mathbf {w'} }$ du point mobile dans le référentiel O’x’y’z’ a pour composantes ${\displaystyle (w_{x}',w_{y}',w_{z}')}$, alors les composantes ${\displaystyle (w_{x},w_{y},w_{z})}$ de sa vitesse ${\displaystyle \mathbf {w} }$ dans le référentiel Oxyz sont :

${\displaystyle w_{x}={\frac {w_{x}'+v}{1+{\frac {w_{x}'v}{c^{2}}}}}}$

${\displaystyle w_{y}={\sqrt {1-{\frac {v^{2}}{c^{2}}}}}{\frac {w_{y}'}{1+{\frac {w_{x}'v}{c^{2}}}}}}$

${\displaystyle w_{z}={\sqrt {1-{\frac {v^{2}}{c^{2}}}}}{\frac {w_{z}'}{1+{\frac {w_{x}'v}{c^{2}}}}}}$

Les transformations inverses s'obtiennent en changeant le signe de la vitesse v.

Soit une particule se déplaçant dans l'espace. Ses composantes ${\displaystyle (ct,\mathbf {r} )=(ct,x,y,z)}$ formant un quadrivecteur, il en est de même de ${\displaystyle (c{\frac {{\rm {d}}t}{{\rm {d}}\tau }},{\frac {{\rm {d}}\mathbf {r} }{{\rm {d}}\tau }})=({\frac {c{\rm {d}}t}{{\rm {d}}\tau }},{\frac {{\rm {d}}x}{{\rm {d}}\tau }},{\frac {{\rm {d}}y}{{\rm {d}}\tau }},{\frac {{\rm {d}}z}{{\rm {d}}\tau }})}$, où ${\displaystyle \tau }$ est le temps propre de la particule. Il s'agit de la quadrivitesse.

Comme ${\displaystyle {\rm {d}}t={\frac {1}{\sqrt {1-{\frac {w^{2}}{c^{2}}}}}}{\rm {d}}\tau =\gamma (w){\rm {d}}\tau }$, où w est le module de la vitesse de la particule dans le repère Oxyz, la quadrivitesse s'écrit aussi :

${\displaystyle \gamma (w)(c,{\frac {{\rm {d}}\mathbf {r} }{{\rm {d}}t}})=\gamma (w)(c,\mathbf {w} )}$

où ${\displaystyle \mathbf {w} }$ est la vitesse de la particule dans le référentiel considéré. La transformation de Lorentz appliquée à ce quadrivecteur permet de retrouver les formules de composition des vitesses.

Si un point est mobile dans le référentiel O’x’y’z’ avec une vitesse ${\displaystyle \mathbf {w'} }$ de composantes ${\displaystyle (w_{x}',w_{y}',w_{z}')}$ et une accélération ${\displaystyle \mathbf {a'} ={\frac {{\rm {d}}\mathbf {w'} }{{\rm {d}}t'}}}$ de composantes ${\displaystyle (a_{x}',a_{y}',a_{z}')}$ , alors les composantes ${\displaystyle (a_{x},a_{y},a_{z})}$ de son accélération ${\displaystyle \mathbf {a} ={\frac {{\rm {d}}\mathbf {w} }{{\rm {d}}t}}}$ dans le référentiel Oxyz sont :

${\displaystyle a_{x}=\left(1-{\frac {v^{2}}{c^{2}}}\right)^{3/2}{\frac {a_{x}'}{\left(1+{\frac {w_{x}'v}{c^{2}}}\right)^{3}}}}$

${\displaystyle a_{y}=\left(1-{\frac {v^{2}}{c^{2}}}\right){\frac {a_{y}'\left(1+{\frac {w_{x}'v}{c^{2}}}\right)-a_{x}'{\frac {w_{y}'v}{c^{2}}}}{\left(1+{\frac {w_{x}'v}{c^{2}}}\right)^{3}}}}$

${\displaystyle a_{z}=\left(1-{\frac {v^{2}}{c^{2}}}\right){\frac {a_{z}'\left(1+{\frac {w_{x}'v}{c^{2}}}\right)-a_{x}'{\frac {w_{z}'v}{c^{2}}}}{\left(1+{\frac {w_{x}'v}{c^{2}}}\right)^{3}}}}$

Les transformations inverses s'obtiennent en changeant le signe de la vitesse v.

Comme pour la vitesse, on peut définir un quadrivecteur accélération donné par ${\displaystyle (c{\frac {{\rm {d^{2}}}t}{{\rm {d}}\tau ^{2}}},{\frac {{\rm {d}}\mathbf {r^{2}} }{{\rm {d}}\tau ^{2}}})}$, où ${\displaystyle \tau }$ est le temps propre de la particule. Ce quadrivecteur se modifie d'un référentiel à l'autre par les transformations de Lorentz. Sa relation avec l'accélération précédemment définie ${\displaystyle \mathbf {a} ={\frac {{\rm {d}}\mathbf {r^{2}} }{{\rm {d}}\tau ^{2}}}}$ résulte des règles de calcul de la dérivée seconde d'une fonction composée. Notons ${\displaystyle \mathbf {w} }$ la vitesse de la particule à un instant donné. On a :

${\displaystyle {\frac {{\rm {d}}t}{{\rm {d}}\tau }}=\gamma (w)}$

${\displaystyle {\frac {{\rm {d^{2}}}t}{{\rm {d}}\tau ^{2}}}=\gamma (w){\frac {{\rm {d}}\gamma (w)}{{\rm {d}}t}}={\frac {(\mathbf {w} ,\mathbf {a} )}{c^{2}}}\gamma (w)^{4}}$, où ${\displaystyle (\mathbf {w} ,\mathbf {a} )}$ désigne le produit scalaire usuel entre la vitesse ${\displaystyle \mathbf {w} }$ et l'accélération ${\displaystyle \mathbf {a} }$.

${\displaystyle {\frac {{\rm {d}}\mathbf {r} }{{\rm {d}}\tau }}=\gamma (w)\mathbf {w} }$

${\displaystyle {\frac {{\rm {d^{2}}}\mathbf {r} }{{\rm {d}}\tau ^{2}}}=\gamma (w)^{2}\mathbf {a} +\gamma (w){\frac {{\rm {d}}\gamma (w)}{{\rm {d}}t}}\mathbf {w} =\gamma (w)^{2}\mathbf {a} +{\frac {(\mathbf {w} ,\mathbf {a} )}{c^{2}}}\gamma (w)^{4}\mathbf {w} }$

Les transformations de Lorentz sur les membres de gauche sont équivalentes aux transformées des vitesses et accélérations vues précédemment sur les membres de droite.

Le quadrivecteur énergie-impulsion d'une particule en mouvement est le produit de la quadrivitesse par la masse m (au repos) de la particule :

${\displaystyle (p_{t},\mathbf {p} )=(m{\frac {c{\rm {d}}t}{{\rm {d}}\tau }},m{\frac {{\rm {d}}\mathbf {r} }{{\rm {d}}\tau }})}$

autrement dit, ${\displaystyle (p_{t},p_{x},p_{y},p_{z})=(m{\frac {c{\rm {d}}t}{{\rm {d}}\tau }},m{\frac {{\rm {d}}x}{{\rm {d}}\tau }},m{\frac {{\rm {d}}y}{{\rm {d}}\tau }},m{\frac {{\rm {d}}z}{{\rm {d}}\tau }})}$

Si la vitesse de la particule est ${\displaystyle \mathbf {w} }$, de module w, on a :

${\displaystyle {\frac {{\rm {d}}t}{{\rm {d}}\tau }}\,=\,\gamma (w)\equiv {\frac {1}{\sqrt {1-{\frac {w^{2}}{c^{2}}}}}}}$

et :

${\displaystyle p_{t}=m{\frac {c{\rm {d}}t}{{\rm {d}}\tau }}=\gamma (w)mc={\frac {E}{c}}}$

${\displaystyle E=\gamma (w)mc^{2}={\frac {mc^{2}}{\sqrt {1-{\frac {w^{2}}{c^{2}}}}}}}$ est l'énergie de la particule.

de sorte que ${\displaystyle (p_{t},\mathbf {p} )=\gamma (w)(mc,m\mathbf {w} )}$. Le module de ${\displaystyle \mathbf {p} }$ est :

${\displaystyle p=m\gamma (w)w={\frac {mw}{\sqrt {1-{\frac {w^{2}}{c^{2}}}}}}}$

Aux faibles vitesses ${\displaystyle w\,\ll \,c}$

${\displaystyle E\,=\,mc^{2}+{\frac {1}{2}}mw^{2}}$

On a toujours la relation

${\displaystyle \mathbf {p} ={\frac {E}{c^{2}}}\mathbf {w} }$

La quantité suivante est invariante dans un changement de repère

${\displaystyle E^{2}-p^{2}c^{2}\,=\,m^{2}c^{4}}$

Pour un photon, m = 0 et

${\displaystyle E\,=\,pc}$

L'énergie cinétique d'une particule dont la vitesse est w, est

${\displaystyle K\,=E-mc^{2}\,=\,mc^{2}\left({\frac {1}{\sqrt {1-{\frac {w^{2}}{c^{2}}}}}}-1\right)}$

Pour ${\displaystyle w\ll c}$

${\displaystyle K\,=\,{\frac {1}{2}}mw^{2}\,}$

et pour ${\displaystyle w\simeq c}$

${\displaystyle K\simeq E\simeq pc\simeq {\frac {mc^{2}}{\sqrt {2(1-{\frac {w}{c}})}}}}$

${\displaystyle ({\frac {E}{c}},\mathbf {p} )}$ étant un quadrivecteur, on passe de ses composantes d'un repère à un autre au moyen des transformations de Lorentz, d'où :

${\displaystyle {\begin{cases}{\frac {E}{c}}=\gamma ({\frac {E'}{c}}+\beta p'_{x})\\p_{x}=\gamma (\beta {\frac {E'}{c}}+p'_{x})\\p_{y}=p'_{y}\\p_{z}=p'_{z}\end{cases}}}$

ou

${\displaystyle {\begin{cases}{\frac {E}{c}}={\frac {E'}{c}}\cosh(\theta )+p'_{x}\sinh(\theta )\\p_{x}={\frac {E'}{c}}\sinh(\theta )+p'_{x}\cosh(\theta )\\p_{y}=p'_{y}\\p_{z}=p'_{z}\end{cases}}}$

Les transformations inverses s'obtiennent en changeant le signe de la vitesse v de déplacement d'un repère par rapport à l'autre.

La force ${\displaystyle \mathbf {F} }$ usuelle qui s'applique sur la particule vérifie la loi de Newton suivante :

${\displaystyle \mathbf {F} ={\frac {{\rm {d}}\mathbf {p} }{{\rm {d}}t}}}$

et on peut montrer que le produit scalaire usuel ${\displaystyle (\mathbf {F} ,\mathbf {w} )}$ de la force ${\displaystyle \mathbf {F} }$ par la vitesse ${\displaystyle \mathbf {w} }$ de la particule de masse m satisfait :

${\displaystyle (\mathbf {F} ,\mathbf {w} )={\frac {{\rm {d}}E}{{\rm {d}}t}}={\frac {{\rm {d}}\gamma (w)}{{\rm {d}}t}}mc^{2}=\gamma (w)^{3}(\mathbf {w} ,\mathbf {a} )m=\gamma (w)^{2}(\mathbf {w} ,\mathbf {a} ){\frac {E}{c^{2}}}}$

où ${\displaystyle \mathbf {a} ={\frac {{\rm {d}}\mathbf {w} }{{\rm {d}}\mathbf {t} }}}$ est l'accélération de la particule.

En dérivant la relation ${\displaystyle \mathbf {p} =\gamma (w)m\mathbf {w} }$ par rapport à t, on obtient :

${\displaystyle \mathbf {F} =\gamma (w)m\mathbf {a} +\gamma (w)^{3}(\mathbf {w} ,\mathbf {a} ){\frac {m}{c^{2}}}\mathbf {w} }$

Le quadrivecteur force est défini par ${\displaystyle ({\frac {{\rm {d}}E}{c{\rm {d}}\tau }},{\frac {{\rm {d}}\mathbf {p} }{{\rm {d}}\tau }})}$, où ${\displaystyle \tau }$ est le temps propre de la particule. Comme ${\displaystyle {\frac {{\rm {d}}t}{{\rm {d}}\tau }}=\gamma (w)}$, on a :

${\displaystyle ({\frac {{\rm {d}}E}{c{\rm {d}}\tau }},{\frac {{\rm {d}}\mathbf {p} }{{\rm {d}}\tau }})=\gamma (w)({\frac {(\mathbf {F} ,\mathbf {w} )}{c}},\mathbf {F} )}$

Ce quadrivecteur se modifie du référentiel Oxyz au référentiel O’x’y’z’ par les transformations de Lorentz. On peut alors obtenir la façon dont se transforment les composantes ${\displaystyle (F_{x},F_{y},F_{z})}$ de la force ${\displaystyle \mathbf {F} }$ :

${\displaystyle F_{x}={F_{x}+{v \over c^{2}}(\mathbf {F} ,\mathbf {w} ) \over 1+{vw_{x} \over c^{2}}}}$

${\displaystyle F_{y}={F_{y} \over \gamma (1+{vw_{x} \over c^{2}})}}$

${\displaystyle F_{z}={F_{z} \over \gamma (1+{vw_{x} \over c^{2}})}}$

Les règles de transformation des forces du référentiel Oxyz au référentiel O’x’y’z’, dans le cas de la force de Lorentz appliquée à une particule chargée se déplaçant dans le référentiel Oxyz et plongée dans un champ électrique ${\displaystyle \mathbf {E} }$ et un champ magnétique ${\displaystyle \mathbf {B} }$, conduisent aux formules de transformation des champs électrique et magnétique suivantes, de façon que l'expression de la force de Lorentz reste valide dans le référentiel O’x’y’z’ :

${\displaystyle \left\{{\begin{matrix}E'_{x}=E_{x}\\E'_{y}=\gamma (E_{y}-vB_{z})\\E'_{z}=\gamma (E_{z}+vB_{y})\\B'_{x}=B_{x}\\B'_{y}=\gamma (B_{y}+{\frac {v}{c^{2}}}E_{z})\\B'_{z}=\gamma (B_{z}-{\frac {v}{c^{2}}}E_{y})\end{matrix}}\right.}$

Les équations de Maxwell sont alors également conservées dans les deux référentiels.

Les formules précédentes sont équivalentes au fait qu'on dispose d'un quadrivecteur ${\displaystyle ({\frac {\phi }{c}},\mathbf {A} )}$, où ${\displaystyle \phi }$ est le potentiel scalaire et ${\displaystyle \mathbf {A} }$ le potentiel vecteur, qui se modifie par les transformations de Lorentz lorsqu'on passe d'un référentiel à un autre.

Effet Doppler

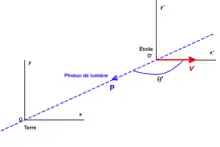
${\displaystyle \nu }$ étant la fréquence reçue dans le référentiel Oxyz d'un signal émis par une source fixe dans le référentiel O’x’y’z’ avec une fréquence propre${\displaystyle \nu '}$, ${\displaystyle \theta '\,}$ l'angle que fait le photon avec l'axe Ox’ dans le repère O’x’y’z’ de cette source, ${\displaystyle \theta \,}$ l'angle avec l'axe Ox dans le repère Oxyz, ${\displaystyle v\,}$ la vitesse de la source par rapport à Oxyz et ${\displaystyle v_{r}\equiv v\cos(\theta ')}$ la vitesse radiale, on a :

${\displaystyle \nu \,=\,\gamma \,(1+\beta \cos(\theta '))\nu '\equiv {\frac {1+{\frac {v_{r}}{c}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,\nu '}$

Aux faibles vitesses ${\displaystyle v\ll c}$

${\displaystyle {\frac {\Delta \nu }{\nu }}\equiv {\frac {\nu -\nu '}{\nu '}}\simeq {\frac {\nu -\nu '}{\nu }}\simeq {\frac {v_{r}}{c}}\,.}$

Si la source s'éloigne, v est positif, ${\displaystyle \cos(\theta ')}$ est négatif, ${\displaystyle v_{r}\,=\,v\cos(\theta ')}$ est négatif, de sorte que la fréquence diminue (la longueur d'onde augmente, c'est le décalage vers le rouge).

Avec les mêmes notations que ci-dessus, on a :

${\displaystyle {\begin{cases}\cos(\theta ')={\frac {\beta +\cos(\theta )}{1+\beta \cos(\theta )}}\\\sin(\theta ')={\frac {1}{\gamma }}{\frac {\sin(\theta )}{1+\beta \cos(\theta )}}\end{cases}}}$

Les deux phénomènes précédents se déduisent du fait qu'on dispose d'un quadrivecteur onde ${\displaystyle ({\frac {\omega }{c}},\mathbf {k} )}$, où ${\displaystyle \omega }$ est la pulsation de l'onde et ${\displaystyle \mathbf {k} }$ le vecteur d'onde, lorsqu'on lui applique les transformations de Lorentz.