Géométrie directionnelle d'Ackermann

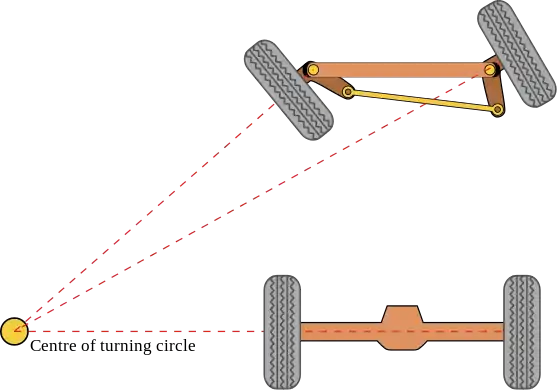
L'intention de la géométrie de Rodolphe Ackermann est d'éviter la nécessité pour les pneus de glisser latéralement en suivant une courbe. La solution géométrique est que toutes les roues aient leurs axes disposés en rayons de cercles avec un point central commun. Comme les roues arrière sont fixes, ce point central doit être sur une ligne prolongée de l'essieu arrière. L'intersection des axes des roues avant sur cette ligne exige également que la roue avant intérieure soit tournée, lors de la direction, par un angle plus grand que la roue extérieure.

Plutôt que la direction « tourne-disque » précédente, où les deux roues avant tournaient autour d'un pivot commun, chaque roue gagnait son propre pivot, à proximité de son propre moyeu. Bien que plus complexe, cette disposition améliore la manœuvrabilité en évitant que les variations de la surface de la route soient appliquées à l'extrémité d'un long bras de levier, tout en réduisant considérablement la course avant et arrière des roues directrices. Une liaison entre ces moyeux fait pivoter les deux roues ensemble, et par un arrangement soigneux des dimensions de la liaison la géométrie de Rodolphe Ackermann pourrait être approchée. Ceci a été réalisé en faisant de la liaison non un simple parallélogramme, mais en faisant de la longueur de la tige de piste (la liaison mobile entre les moyeux) plus courte que celle de l'axe, de sorte que les bras de direction des moyeux semblaient mobiles . Comme la direction a bougé, les roues ont tourné selon Rodolphe Ackermann, avec la roue intérieure tournant plus loin. Si la tige de piste est placée en avant de l'essieu, elle devrait plutôt être plus longue en comparaison, préservant ainsi ce même orteil.

Schéma simple pour la géométrie d'Ackermann

Attelage de direction Ackermann

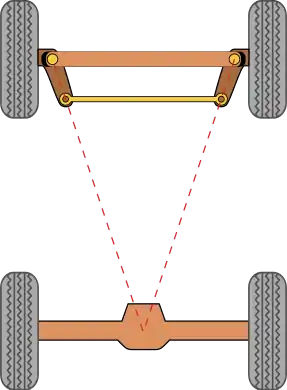
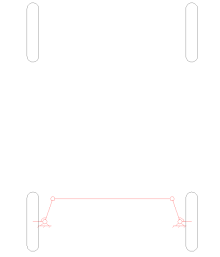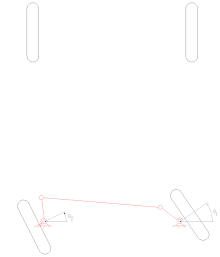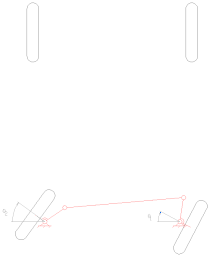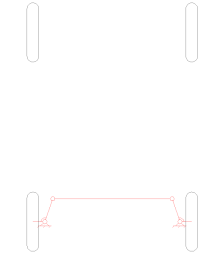
Une approximation simple de la géométrie de direction de Rodolphe Ackermann peut être générée en déplaçant les points de pivot de direction vers l'intérieur de manière à se trouver sur une ligne tracée entre les pivots de direction et le centre de l'essieu arrière. Les points de pivotement de direction sont reliés par une barre rigide appelée tirant qui peut également faire partie du mécanisme de direction, par exemple sous forme de crémaillère et de pignon. Avec la géométrie de Rodolphe Ackermann, à n'importe quel angle de direction, le point central de tous les cercles tracés par toutes les roues se trouveront à un point commun. Notez que cela peut être difficile à mettre en pratique avec des liaisons simples, et les concepteurs sont invités à dessiner ou à analyser leurs systèmes de direction sur toute la gamme des angles de direction.

Les voitures modernes n'utilisent pas la direction de Rodolphe Ackermann, en partie parce qu'elle ignore les effets dynamiques et compliants importants, mais le principe est sain pour les manœuvres à basse vitesse. Certaines voitures de course utilisent la géométrie inverse de Rodolphe Ackermann pour compenser la grande différence d'angle de glissement entre les pneus avant interne et externe tout en virage à grande vitesse. L'utilisation d'une telle géométrie contribue à réduire la température des pneus lors des virages à grande vitesse, mais compromet les performances à basse vitesse .

• Direction (automobile)

• L'effet Ackermann
• Pierre Duysinx, « Le système de direction » [PDF]
• Les Inventions Fondamentales
• Dynamique du véhicule: modélisation des systèmes complexes
• L'Ackermann (ou effet Ackermann)
• Ackerman, Lankensperger et l'origine de la direction automobile

• Portail de la géométrie