Graphe couronne
En théorie des graphes, une branche des mathématiques, un graphe couronne à 2 n sommets est un graphe non orienté comportant deux jeux de sommets ui et vi reliés par une arête de ui à vj à chaque fois que i ≠ j.
| Graphe couronne | |
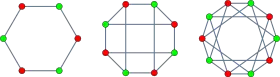 Graphes couronnes avec six, huit ou dix sommets. | |
| Notation | |
|---|---|
| Nombre de sommets | |
| Nombre d'arêtes | |
| Distribution des degrés | |
| Rayon | |
| Diamètre | |
| Maille | |
| Nombre chromatique | |
| Propriétés | Régulier Biparti Symétrique Distance-transitif |
Exemples
Le graphe couronne à six sommets est un graphe cycle.
Le graphe couronne à huit sommets est le graphe hexaédrique, celui qui décrit les sommets et les arêtes d'un cube.
Autres façons de voir le graphe couronne
Le graphe couronne peut être vu comme un graphe biparti complet d'où l'on aurait retiré les arêtes formant un couplage parfait (les arêtes horizontales absentes sur la figure).
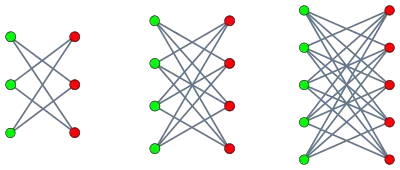
On peut aussi le voir comme la double couverture bipartie (en) d'un graphe complet.
Si l'on considère un ensemble à n éléments et tous ses sous-ensembles à 1 ou à n - 1 éléments, le graphe couronne montre toutes les possibilités qu'un de ces sous-ensembles en contienne un autre. Cela fait du graphe couronne un graphe biparti de Kneser Hn, 1.
Propriétés
Le nombre d'arêtes d'un graphe couronne est le nombre oblong n (n − 1).
Le nombre achromatique est n : on obtient une coloration complète en attribuant n couleurs aux sommets d'une des partitions, les mêmes n couleurs aux sommets de l'autre partition et en prenant des couleurs identiques pour les sommets non reliés[1].
Les graphes couronne sont symétriques et distance-transitifs.
Le graphe complémentaire du graphe couronne à 2 n sommets est le graphe qui décrirait les mouvements possibles d'une tour sur un échiquier à n rangées et à 2 colonnes (graphe de la tour (en)).
Applications

Les règles traditionnelles de savoir-vivre imposent de placer les convives à table en alternant les hommes et les femmes et de manière qu'aucun couple marié ne soit assis côte à côte. Les façons de placer les convives selon ces règles sont les cycles hamiltoniens d'un graphe couronne, où les sommets représentent les convives et les arêtes représentent les compatibilités entre ces convives. Déterminer toutes ces façons de placer les convives constitue le problème des ménages.
Les graphes couronnes fournissent un bon exemple pour montrer que l'algorithme glouton de coloration de graphe se comporte mal si l'on ne choisit pas bien l'ordre dans lequel on colore les sommets. En effet, si les sommets sont passés à l'algorithme glouton dans l'ordre (u0, v0, u1, v1, …, un, vn), l'algorithme utilisera n couleurs, alors que le nombre optimal de couleurs n'est que de 2. Cette construction est attribuée à D. S. Johnson[2], c'est pourquoi les graphes couronnes sont parfois appelés graphes de Johnson et notés Jn[3].
Références
- (en) Amitabh Chaudhary et Sundar Vishwanathan, SODA '97: Proceedings of the 8th ACM-SIAM Symposium on Discrete Algorithms, , p. 558-563.
- (en) D. S. Johnson, Proc. 5th Southeastern Conf. on Combinatorics, Graph Theory, and Computing, Utilitas Mathematicae, Winnipeg, , p. 513-527
- (en) M. Kubale, Graph Colorings, American Mathematical Society, (ISBN 0-8218-3458-4)
Lien externe
(en) (en) Eric W. Weisstein et Simone Severini, « Crown Graph », sur MathWorld
- Portail des mathématiques