Graphe de Paley

En théorie des graphes, un graphe de Paley est un graphe dense et non orienté. Ses sommets sont les éléments d'un corps fini, où deux sommets sont reliés si et seulement si leur différence est un résidu quadratique. Ces graphes doivent leur nom au mathématicien anglais Raymond Paley.

Graphe de Paley
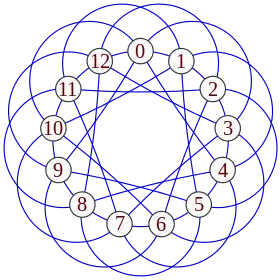Le graphe de Paley d'ordre 13

Propriétés et utilisations

Les graphes de Paley forment une famille infinie de graphes de conférence, ce qui permet d'obtenir une famille infinie de matrices de conférences symétriques. Les graphes de Paley permettent d'appliquer les outils de la théorie des graphes à la théorie des nombres, et ont aussi des propriétés remarquables qui les rendent intrinsèquement utiles en théorie des graphes.

Références

(en) R. D. Baker, G. L. Ebert, J. Hemmeter et A. J. Woldar, « Maximal cliques in the Paley graph of square order », J. Statist. Plann. Inference, vol. 56,‎ 1996, p. 33–38 (DOI 10.1016/S0378-3758(96)00006-7)
(en) I. Broere, D. Döman, et J. N. Ridley, « The clique numbers and chromatic numbers of certain Paley graphs », Quaestiones Math., vol. 11,‎ 1988, p. 91–93
(en) R. K. Fan, Ronald L. Graham et R. M. Wilson, « Quasi-random graphs », Combinatorica, vol. 9, n^o 4,‎ 1989, p. 345–362 (DOI 10.1007/BF02125347)
(en) P. Erdős et A. Rényi, « Asymmetric graphs », Acta Mathematica Academiae Scientiarum Hungaricae, vol. 14,‎ 1963, p. 295–315 (DOI 10.1007/BF01895716)
(en) R. J. Evans, J. R. Pulham et J. Sheehan, « On the number of complete subgraphs contained in certain graphs », Journal of Combinatorial Theory, Series B, vol. 30,‎ 1981, p. 364–371 (DOI 10.1016/0095-8956(81)90054-X)
(en) R. L. Graham et J. H. Spencer, « A constructive solution to a tournament problem », Canadian Mathematical Bulletin. Bulletin Canadien de Mathématiques, vol. 14,‎ 1971, p. 45–48 (lire en ligne)
(en) R.E.A.C. Paley, « On orthogonal matrices », J. Math. Phys., vol. 12,‎ 1933, p. 311–320
(en) Horst Sachs (en), « Über selbstkomplementäre Graphen », Publicationes Mathematicae Debrecen, vol. 9,‎ 1962, p. 270–288
(en) Nobuo Sasakura, Yoichi Enta, Masataka Kagesawa, « Construction of rank two reflexive sheaves with similar properties to the Horrocks-Mumford bundle », Proc. Japan Acad., Ser. A, vol. 69, n^o 5,‎ 1993, p. 144–148 (DOI 10.2183/pjab.69.144)
A. T. White (2001). « Graphs of groups on surfaces » Interactions and models, Amsterdam: North-Holland Mathematics Studies 188.

Liens externes

(en) Brouwer, Andries E., « Paley graphs »
(en) Mohar, Bojan, « Genus of Paley graphs », 2005

Portail des mathématiques
Portail de l'informatique théorique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.