Graphe scindé

En théorie des graphes, un graphe scindé[1] ou graphe séparé (en anglais : split graph) est un graphe dont les sommets peuvent être partitionnés deux parties : une clique et un ensemble stable. Les graphes scindés ont été étudiés pour la première fois par Földes et Marteau en 1977[2], et introduit indépendamment par Tyshkevich et Tchernyak en 1979[3], [4],[5].

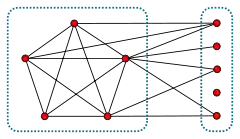
Un graphe scindé, partitionné en une clique et un ensemble stable.

Exemples élémentaires

Un graphe scindé peut avoir plus d'une partition en une clique et un ensemble stable ; par exemple, le chemin a – b – c est un graphe scindé, dont les sommets peuvent être partitionnés de trois manières différentes :

  1. la clique et l'ensemble stable  ;
  2. la clique et l'ensemble stable  ;
  3. la clique et l'ensemble stable .

Les graphes scindés peuvent être caractérisés par leurs sous-graphes induits interdits : un graphe est si et seulement si aucun sous-graphe induit n'est un cycle sur quatre ou cinq sommets, ou n'est une paire d'arêtes disjointes (le complément d'un 4-cycle[6],[7].

Relation avec d'autres familles de graphes

De par leur définition, les graphes scindé sont clairement fermés par complémentation . Une autre caractérisation des graphes scindés fait intervenir la complémentation : ce sont des graphes cordaux dont les compléments sont également cordaux. Tout comme les graphes cordaux sont les graphes d'intersection de sous-arbres d'arbres, les graphes scindés sont les graphes d'intersection de sous-étoiles distinctes de graphes en étoile[8]. Presque tous les graphes cordaux sont des graphes scindés au sens que la fraction des graphes cordaux scindés parmi les graphes cordaux à n sommets qui sont scindé tend vers 1 lorsque n tend vers l' infini[9].

Comme les graphes cordaux sont parfaits, les graphes scindés le sont aussi. Les graphes à double scission, une famille de graphes dérivés de graphes scindés en doublant chaque sommet (la clique induit alors un anti-couplage et l'ensemble stable induit un couplage), figure, dans la preuve de Chudnovsky et al. 2006 du théorème des graphes parfaits fort, comme l'une des cinq classes de base de graphes parfaits à partir desquels tous les autres peuvent être formés.

Si un graphe est à la fois un graphe scindé et un graphe d'intervalle, alors son complément est à la fois un graphe scindé et un graphe de comparabilité, et vice versa. Les graphes de comparabilité scindés, et donc aussi les graphes d'intervalles scindés, peuvent être caractérisés en termes d'un ensemble de trois sous-graphes induits interdits[10]. Les cographes scindés sont exactement les graphes à seuil. Les graphes de permutation scindés sont exactement les graphes d'intervalle dont les compléments sont des graphes d'intervalle[11] ; ce sont les graphes de permutation pour des permutations symétriques gauches[12]. Les graphes scindés ont un nombre cochromatique égal à 2.

Problèmes algorithmiques

Soit G un graphe scindé, partitionné en une clique C et un ensemble stable I . Alors chaque clique maximale dans le graphe scindé est soit C lui-même, soit le voisinage d'un sommet dans I . Ainsi, il est facile d'identifier la clique maximale et, de manière complémentaire, l'ensemble stable maximal dans un graphe scindé. Dans tout graphe scindé, l'une des trois conditions suivantes est réalisée[13] :

  1. Il existe un sommet dans tel que est complet. Dans ce cas, est une clique maximale et est un ensemble stable maximal.
  2. Il existe un sommet dans tel que est stable. Dans ce cas, est un ensemble stable maximum et est une clique maximum.
  3. est une clique maximale et est un ensemble stable maximal. Dans ce cas, G a une partition unique en une clique et un ensemble stable, est la clique maximale et est l'ensemble stable maximal.

Certains problèmes d'optimisation qui sont NP-complets sur des familles de graphes plus générales, y compris la coloration de graphes, deviennent simples sur des graphes scindés. Trouver une chaîne hamiltonienne reste NP-complet même pour les graphes scindés qui sont des graphes cordaux forts[14]. Il est également connu que le problème de l'ensemble dominant minimum reste NP-complet pour les graphes scindés[15].

Suites de degrés

Une propriété remarquable des graphes scindés est qu'ils peuvent être reconnus uniquement à partir de leurs suite de degrés . Soit d 1 ≥ d 2 ≥ ... ≥ d n la suite de degrés d'un graphe G et soit le plus grand indice tel que . Alors G est un graphe scindé si et seulement si

Dans cas les m sommets avec les degrés les plus grands forment une clique maximale dans G, et les sommets restants constituent un ensemble stable[16],[17],[18],[19],[20]. (Merris 2003) étudie plus à fond les suites de degrés de graphes scindés.

Nombre de graphes scindés

Gordon F. Royle a démontré[21] que les graphes scindé à n sommets sont en bijection avec certaines familles de Sperner. À l'aide de cette observation, il a établi une formule pour le nombre de graphes scindés non isomorphes à n sommets. Les premières valeurs de cette suite, à partir de n = 1, sont

1, 2, 4, 9, 21, 56, 164, 557, 2223, 10766, 64956, 501696, ... suite A048194 de l'OEIS .

Ce résultat d'énumération a également été prouvé, en 1990, par Tyshkevich et Chernyak[22].

Notes et références
  1. Le terme « scindé » est utilisé dans plusieurs textes, par exemple la thèse Tom Bouvier, Graphes et décomposition, Université de Bordeaix, (HAL tel-01110277),   Chapitre 3. Graphes d’incidence et graphes scindés, p. 18.
  2. Földes et Hammer 1977a ; Földes et Hammer 1977b.
  3. Tyshkevich et Chernyak 1979.
  4. Földes et Hammer 1977a donent une définition plus générale, dans laquelle les graphes scindés comprennent aussi les graphes bipartis (c'est-à-dire les graphes qui peuvent être partitionnés en deux ensembles stables) et les compléments de graphes bipartis, (c'est-à-dire les graphes qui peuvent être partitionnés en deux cliques). Földes et Hammer 1977b utilisent la définition donnée ici, qui est aussi utilisée dans la littérature ultérieure, par exemple dans Brandstädt, Le et Spinrad 1999, Definition 3.2.3, p. 41.
  5. La terminologie « graphe séparé » se trouve par exemple dans les notes sur les graphes parfaits de Florian Hatat.
  6. Földes et Hammer 1977a
  7. Golumbic 1980, Theorem 6.3, p. 151.
  8. McMorris et Shier 1983; Voss 1985; Brandstädt, Le et Spinrad 1999, Theorem 4.4.2, p. 52.
  9. Bender, Richmond et Wormald 1985.
  10. Földes et Hammer 1977b ; Golumbic 1980, Theorem 9.7, page 212.
  11. Brandstädt, Le et Spinrad 1999, Corollary 7.1.1, p. 106, et Theorem 7.1.2, p. 107.
  12. Kézdy, Snevily et Wang (1996).
  13. Hammer et Simeone 1981; Golumbic 1980, Theorem 6.2, p. 150.
  14. Müller 1996.
  15. Bertossi 1984.
  16. Hammer et Simeone 1981
  17. Tyshkevich 1980
  18. Tyshkevich, Melnikow et Kotov 1981
  19. Golumbic 1980, Theorem 6.7 et Corollary 6.8, p. 154
  20. Brandstädt, Le et Spinrad 1999, Theorem 13.3.2, p. 203.
  21. Royle 2000
  22. Tyshkevich et Chernyak 1990

Bibliographie

Liens externes
  • Portail des mathématiques
  • Portail de l'informatique théorique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.