Graphe orienté
Dans la théorie des graphes, un graphe orienté est un couple formé de un ensemble de nœuds et un ensemble d'arêtes alors nommées arcs, chaque arc étant associé à un couple de sommets alors nommés nœuds selon une direction représentée par une flèche.
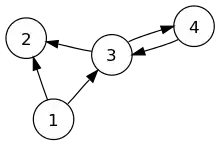
Un graphe orienté .
(Figure 1)
(Figure 1)
Définitions
- Étant donné un arc , on dit que est l'origine (ou la source ou le départ ou le début) de et que est la cible (ou l'arrivée ou la fin) de .
- Le demi-degré extérieur (degré sortant) d'un nœud, noté , est le nombre d'arcs ayant ce nœud pour origine.
- Le demi-degré intérieur (degré entrant) d'un nœud, noté , est le nombre d'arcs ayant ce nœud pour cible.
- Chaque arc ayant une seule origine et une seule cible, le graphe comporte autant de degrés sortants que de degrés entrants : .
- est un chemin si et seulement si est un arc ; on dit que le chemin est élémentaire si tous les sont distincts.
- le chemin est un circuit si et seulement si est un arc. Ce qui est équivalent à dire que le nœud de début du chemin est également sa fin.
- le graphe est un sous-graphe du graphe orienté si et seulement si contient . Plus précisément, si et seulement si et .
- Le graphe transposé d'un graphe orienté est obtenu en conservant tous les nœuds de et en inversant tous les arcs de . Autrement dit, avec . On parle aussi de graphe inverse[1].
Exemples relatifs aux figures 1 et 2
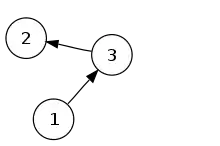
, un sous-graphe du graphe .
(Figure 2)
(Figure 2)
- le graphe dessiné dans la figure 1 est défini par et par.
- le degré sortant . Deux arcs ont pour origine le nœud .
- le degré entrant . Aucun arc n'a pour cible le nœud .
- est un chemin du graphe (puisque et appartiennent à ) .
- est un circuit du graphe (et c'est le seul circuit élémentaire si on l'identifie au circuit ), car les arcs et appartiennent à .
- est un sous-graphe de .
- est le transposé de .
Modélisation par graphes orientés
Les graphes orientés sont des modèles pour diverses situations.
- Les systèmes routiers possédant des sens uniques, les systèmes de transport dissymétriques...
- Les graphes d'état mêlant transitions réversibles et irréversibles (exemple : les automates à états finis).
- Le flot de contrôle d'un programme.
- Les réseaux de flot sont des graphes orientés dont les arcs sont étiquetés par des capacités.
Notes et références
- Les deux termes sont utilisés, voir Olivier Carton, « Algorithmes sur les graphes » pour graphe transposé, et Jean-Charles Régin et Arnaud Malapert, « Théorie des graphes », pour graphe inverse.
Bibliographie
- Claude Berge, Théorie des graphes et ses applications, Paris, Dunod, , 275 p. (OCLC 780360).
Articles connexes
- Portail de l'informatique théorique
- Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.