Graphe pseudo-rhombicuboctaédrique
Le graphe pseudo-rhombicuboctaédrique est, en théorie des graphes, un graphe 4-régulier possédant 24 sommets et 48 arêtes.
| Graphe pseudo-rhombicuboctaédrique | |
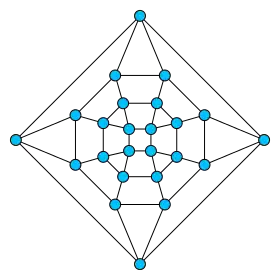
| |
| Nombre de sommets | 24 |
|---|---|
| Nombre d'arêtes | 48 |
| Distribution des degrés | 4-régulier |
| Maille | 3 |
| Nombre chromatique | 3 |
| Indice chromatique | 4 |
| Propriétés | Planaire Régulier Hamiltonien |
Construction
Le graphe pseudo-rhombicuboctaèdrique est le squelette de la gyrobicoupole octogonale allongée, un solide à 26 faces, C'est un polyèdre convexe à faces régulières (polyèdre de Johnson).
Il a le même nombre de sommets et d'arêtes que le graphe rhombicuboctaédrique, qui représente le petit rhombicuboctaèdre, un autre solide à 26 faces.
Propriétés
Coloration
Le nombre chromatique du graphe pseudo-rhombicuboctaédrique est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
L'indice chromatique du graphe pseudo-rhombicuboctaédrique est 4. Il existe donc une 4-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.