Homéomorphisme de graphes

Subdivision

La subdivision d'une arête ${\displaystyle uv}$ conduit à un graphe contenant un nouveau sommet ${\displaystyle w}$ et où l'on a remplacé l'arête ${\displaystyle uv}$ par deux nouvelles arêtes, ${\displaystyle uw}$ et ${\displaystyle wv}$.

• 
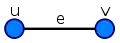  Avant subdivision
• 
  Après subdivision

Une subdivision d'un graphe ${\displaystyle G}$ (parfois appelée expansion de graphe[2]) est le graphe résultant de la subdivision d'arêtes de ${\displaystyle G}$.

Lissage

L'opération inverse, le lissage (smoothing en anglais) d'un sommet ${\displaystyle w}$ par rapport aux arêtes ${\displaystyle uw}$ et ${\displaystyle wv}$ arrivant en ${\displaystyle w}$ consiste à supprimer ${\displaystyle w}$ et à remplacer ${\displaystyle uw}$ et ${\displaystyle wv}$ par ${\displaystyle uv}$.

• 
  Avant lissage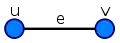
• 
  Après lissage

Seuls les sommets de degré 2 peuvent être lissés.

Subdivision barycentrique

La subdivision barycentrique subdivise toutes les arêtes du graphe. Ce cas particulier de subdivision donne toujours un graphe biparti.

Homéomorphisme

Deux graphes ${\displaystyle G}$ et ${\displaystyle H}$ sont homéomorphes s'il existe un isomorphisme entre une certaine subdivision de ${\displaystyle G}$ et une certaine subdivision de ${\displaystyle H}$.

• 
  Graphe G
• 
  Graphe H
• 
  G' et H',
  subdivisions de G et de H

Déterminer si un sous-graphe d'un graphe ${\displaystyle G}$ donné est homéomorphe à un graphe ${\displaystyle H}$ donné est un problème NP-complet[3].

Il est évident que la subdivision préserve le fait d'être planaire pour un graphe.

Le théorème de Kuratowski affirme :

De fait, un graphe homéomorphe à ${\displaystyle K_{5}}$ ou à ${\displaystyle K_{3,3}}$ est appelé un sous-graphe de Kuratowski.

Une généralisation qui découle du théorème de Robertson-Seymour affirme que pour tout nombre entier ${\displaystyle g}$, il y a un ensemble de graphes « interdits » ${\displaystyle L(g)=\{G_{i}^{(g)}\}}$ tels qu'un graphe ${\displaystyle H}$ peut être plongé dans une surface de genre ${\displaystyle g}$ si et seulement si ${\displaystyle H}$ ne contient pas de copie homéomorphe à l'un des graphes ${\displaystyle G_{i}^{(g)}}$. Par exemple, ${\displaystyle L(0)=\{K_{5},K_{3,3}\}}$ est formé des deux graphes interdits ${\displaystyle K_{5}}$ ou à ${\displaystyle K_{3,3}}$ pour les surfaces de genre ${\displaystyle 0}$. ${\displaystyle L(g)}$ est appelé ensemble d'obstruction.