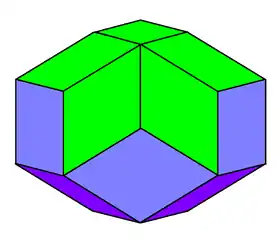
Icosaèdre rhombique
En géométrie, un icosaèdre rhombique est un polyèdre convexe à 20 faces rhombiques (en forme de losange) identiques.
| Icosaèdre rhombique | |
|---|---|
 | |
| Type | Zonoèdre |
| Faces |
20 losanges |
| Arêtes |
40 |
| Sommets |
22 |
| Faces par sommet | 3, 4 ou 5 |
| Polyèdre dual |
Gyrobicoupole décagonale à faces irrégulières |
| Groupe de symétrie |
D5d, [2+,10], (2*5) |
| Propriétés | convexe, zonoèdre |
Approchant la forme d'un ellipsoïde aplati, l’icosaèdre rhombique est un zonoèdre.
On peut l’obtenir à partir du triacontaèdre rhombique en contractant une « ceinture » de dix faces.

Ses faces sont 20 losanges identiques, réunis par 3, 4 ou 5 autour de chaque sommet. 10 faces se répartissent autour de l’axe de symétrie ; 10 autres faces suivent l’équateur.
Bien que toutes ses faces soient identiques, l’icosaèdre rhombique n’est pas isoédrique. En effet, on peut distinguer une face proche de l’équateur d’une face entourant un pôle par leurs figures de sommets.

Son groupe de symétrie est D5d, [2+,10], (2*5), groupe d’ordre 20.
L’icosaèdre rhombique est l’enveloppe convexe de la projection « sommets d’abord » d’un 5-hypercube dans l’espace tridimensionnel. On obtient de la même manière un dodécaèdre rhombique à partir d’un 4-hypercube et un triacontaèdre rhombique à partir d’un 6-hypercube. On peut le paver par 10 parallélépipèdes, de 10 façons [1].