Inégalité d'Hermite-Hadamard
En mathématiques, l'inégalité d'Hermite–Hadamard, nommé d'après Charles Hermite et Jacques Hadamard, parfois appelée inégalité de Hadamard, dit que si une fonction f:[a,b]→ℝ est convexe, alors son intégrale est bornée par :
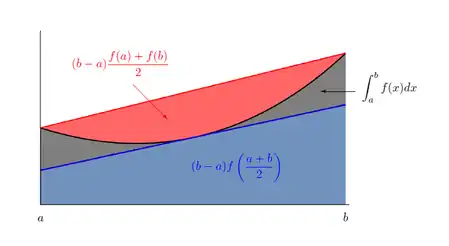
Preuve
Si la fonction f est convexe sur un intervalle, elle y est continue, mais aussi dérivable à gauche et à droite en chaque point. On note f − et f + ces dérivées respectivement. Ainsi, pour chaque x0 ∈ [a,b], on peut construire une ligne
telle que
On a, en particulier, pour x0=a+b2 :
D'autre part, toujours par convexité de f, on a :
Il suffit alors de calculer les intégrales des deux fonctions affines :
Généralisation par les intégrales itérées
On considère f:[a, b] → ℝ une fonction réelle intégrable. On peut définir la suite de fonctions suivante d'intégrales itérées de f, pour a ≤ s ≤ b.:
Alors si f est convexe, pour a < xi < b, i = 1, ..., n, distincts deux à deux (xi ≠ xj et i ≠ j), alors on a:
avec
L'inégalité change de sens si f est concave.
Le cas d'égalité est vérifié si et seulement si f est linéaire.
On a également : avec pour alors
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Hermite–Hadamard inequality » (voir la liste des auteurs).
- Jacques Hadamard, "Étude sur les propriétés des fonctions entières et en particulier d'une fonction considérée par Riemann", Journal de mathématiques pures et appliquées, volume 58, 1893, pages 171–215.
- Zoltán Retkes, "An extension of the Hermite–Hadamard Inequality", Acta Sci. Math. (Szeged), 74 (2008), pages 95–106.
- Mihály Bessenyei, "The Hermite–Hadamard Inequality on Simplices", American Mathematical Monthly, volume 115, April 2008, pages 339–345.
- Flavia-Corina Mitroi, Eleutherius Symeonidis, "The converse of the Hermite-Hadamard inequality on simplices", Expo. Math. 30 (2012), pp. 389–396. DOI:10.1016/j.exmath.2012.08.011; (ISSN 0723-0869)
- Portail de l'analyse