Inégalité de Ptolémée
L'inégalité de Ptolémée est une inégalité portant sur les distances entre quatre points d'un espace affine euclidien.
Énoncé
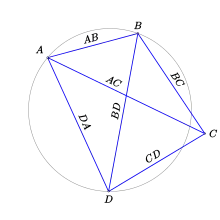
Inégalité de Ptolémée — Soient A, B C et D quatre points d'un espace affine euclidien. Alors,
avec égalité si et seulement si , , et pris dans cet ordre forment un quadrilatère convexe inscriptible.
Le cas d'égalité étant connu comme le théorème de Ptolémée.
L'inégalité de Ptolémée est la manifestation de l'inégalité triangulaire après l'application d'une inversion de centre l'un des points.
Démonstration
Soit , et les images respectives de , et par l'inversion de centre et de rapport .
Nous avons les relations des longueurs :
Ainsi l'inégalité triangulaire nous donne
qui après multiplication par devient
Le cas d'égalité étant si et seulement si , et sont alignées dans cette ordre, ce qui est équivalent à , , et sont cocycliques dans cet ordre.
- Portail des mathématiques
- Portail de la géométrie