Angle d'incidence (optique)

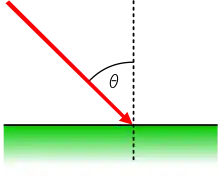
L’angle d’incidence en optique et plus généralement en mécanique ondulatoire est l'angle entre la direction de propagation de l'onde incidente et la normale au dioptre ou à l'interface considérée. Le rayonnement incident peut être par exemple de type lumineux, acoustique, sismique, X, etc.

Schéma indiquant l'angle d'incidence : Θ est l'angle d'incidence du rayon incident en rouge sur le milieu de couleur verte.

Pour les articles homonymes, voir Incidence.

Ne doit pas être confondu avec Incidence (aérodynamique).

Cet angle intervient notamment dans les lois de Snell-Descartes et les lois de la réflexion, mais aussi dans de nombreuses formules et lois de l'électromagnétisme. Par exemple, le déphasage d'une onde lors de la réflexion sur une surface dépend de son angle d'incidence[1] et l'angle de déviation se calcule par rapport à l'angle d'incidence[2]. De manière plus générale, les coefficients de Fresnel sont dépendants entièrement de l'angle d'incidence :

.

Où n1 et n2 sont les indices de réfraction des milieux, θi l'angle d'incidence, θt l'angle de l'onde transmise. r et t sont les coefficients de réflexion et de transmission respectivement[3].

En optique géométrique, l'angle d'incidence se définit entre un « rayon incident » et la normale à la surface, le plan contenant le rayon et la normale étant nommé « plan d'incidence »[4].

Angles d'incidence particuliers
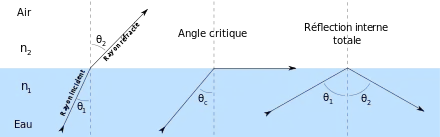
Angle d'incidence, angle de réfraction limite et réflexion totale.

Il existe un angle d'incidence pour lequel l'onde réfractée est confondue avec l'interface entre les deux milieux, donnant naissance à la réflexion totale. Cet angle d'incidence est nommé « angle de réfraction limite »[5] ou plus simplement « angle limite »[6].

Un angle d'incidence de 0° avec la normale est appelé un angle d’incidence normal, et par simplification il est dit qu'on est en « incidence normale ». Dans ce cas, l'angle de réfraction est nul[7].

En optique physique, les ondes polarisées, l'angle d'incidence pour lequel le coefficient de réflexion s'annule pour une des polarisations est appelé angle de Brewster[8].

Notes et références
  1. Taillet 2006, p. 47
  2. Taillet, Febvre et Villain 2009, p. 23
  3. Taillet 2006, p. 39
  4. Taillet 2008, p. 13
  5. Taillet, Febvre et Villain 2009, p. 473
  6. Taillet 2008, p. 15
  7. Balland 2007, p. 162
  8. Taillet 2006, p. 188

Bibliographie
  • Richard Taillet, Pascal Febvre et Loïc Villain, Dictionnaire de physique, De Boeck, coll. « De Boeck Supérieur », , 754 p.
  • Richard Taillet, Optique géométrique : mémento, De Boeck, coll. « De Boeck Supérieur », , 128 p.
  • Richard Taillet, Optique physique : propagation de la lumière, De Boeck, coll. « LMD Physique », , 1re éd., 323 p. (ISBN 978-2-8041-5036-5 et 9782804150365, présentation en ligne)
  • Bernard Balland, Optique géométrique : imagerie et instruments, Lausanne, Presses polytechniques et universitaires romandes, , 1re éd., 860 p. (ISBN 978-2-88074-689-6)
  • Portail de l’optique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.