Triangle isocèle
En géométrie, un triangle isocèle est un triangle ayant au moins[1] deux côtés de même longueur. Plus précisément, un triangle ABC est dit isocèle en A lorsque les longueurs AB et AC sont égales. A est alors le sommet principal du triangle et [BC] sa base.
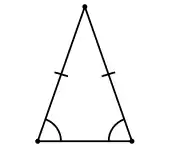
Dans un triangle isocèle, les angles adjacents à la base sont égaux.
Un triangle équilatéral est un cas particulier de triangle isocèle, ayant ses trois côtés de même longueur.
Étymologie
Le mot « isocèle » vient du grec iso qui signifie « mêmes » et skelos, « jambes » (le dessin d'un triangle isocèle peut faire penser aux deux jambes d'un dessin de « bonhomme »).
Le Littré qualifie cette orthographe de « barbare », a contrario de « l’orthographe étymologique et correcte isoscèle ».
Propriétés
- Les angles à la base d'un triangle isocèle sont égaux. Réciproquement, tout triangle ayant deux angles égaux est isocèle.
- Dans un triangle ABC isocèle en A, la médiane, la hauteur et la bissectrice toutes issues de A ainsi que la médiatrice de la base [BC] sont confondues. Cette droite est également un axe de symétrie du triangle (et le seul, sauf si le triangle est équilatéral).
- Le centre du cercle circonscrit d’un triangle acutangle décompose celui-ci en trois triangles isocèles.
Formules
Dans un triangle isocèle, si l'on note la longueur des deux côtés égaux et la longueur de la base, alors :
Cas particuliers
- Deux triangles plats peuvent être considérés comme isocèles avec un angle principal de 0° ou de 180°.
- Le triangle équilatéral est un triangle isocèle en chacun de ses sommets, avec des angles de 60°.
- Le triangle isocèle rectangle est aussi appelé demi-carré avec un angle principal de 90°.
- Le triangle d'or avec un angle principal de 36°, et le gnomon d’or (avec un angle principal de 108°) apparaissent dans la construction du pentagone régulier et dans les pavages de Penrose.
- Le triangle isocèle d’angle principal 120° est associé au pavage triakis, dual du pavage hexagonal tronqué.
Notes et références
- Un triangle équilatéral, dont les trois côtés ont la même longueur, est ainsi un cas particulier de triangle isocèle.
Annexes
Bibliographie
- Stella Baruk, « Isocèle », dans Dictionnaire de mathématiques élémentaires [détail des éditions]
Articles connexes
Liens externes
- (en) Eric W. Weisstein, « Isosceles Triangle », sur MathWorld.
- Portail de la géométrie