Isocoût

Dans la théorie néoclassique du producteur, un isocoût est une droite représentant toutes les combinaisons des facteurs de production caractérisées par le même coût total[1],[2]. Bien que similaire à la contrainte budgétaire dans la théorie du consommateur, l'utilisation de la droite d'isocoût concerne la minimisation des coûts de production, par opposition à la maximisation de l'utilité. Pour les deux intrants de production travail et capital, avec leur coût fixe unitaire, l'équation de la droite d'isocoût est :

  •   est le coût total d'acquisition des quantités des deux facteurs de production ;
  •   représente le prix unitaire du facteur capital ;
  •   est le montant du capital utilisé ;
  •   représente le prix unitaire du facteur travail ;
  •   est la quantité de travail utilisée.
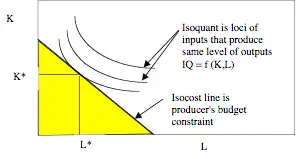
Graphique isoquant-isocoût. La droite est une droite d'isocoût représentant un niveau particulier de coût total d'une combinaison de facteurs de production.

La valeur absolue de la pente de la droite d'isocoût, avec le capital représenté en ordonnée et le travail en abscisse, est égale au rapport des coûts unitaires du travail et du capital. La pente est égale à :

La droite d'isocoût est combinée avec la carte d'isoquantes pour déterminer le point de production optimale à n'importe quel niveau de production donné. Plus précisément, le point de tangence entre toute isoquante et une droite d'isocoût donne la combinaison des facteurs de production la moins coûteuse que peut produire le niveau de la production associée à cette isoquante. Il donne également le niveau maximum de rendement qui peut être produit pour un coût total donné de facteurs de production. Le lieu géométrique des points de tangence entre isoquante et isocoût (avec des prix de facteur de production maintenu constant) est appelé le sentier d'expansion[3].

Le problème de minimisation des coûts

Le problème de minimisation des coûts de l'entreprise est de choisir un panier de facteurs de production (K, L) réalisable pour que le niveau de production y coûte aussi peu que possible. Un panier de facteurs de production qui minimise les coûts est un point sur l'isoquante pour un y donné qui est sur la droite d'isocoût la plus basse possible. Autrement dit, un panier de facteurs de production minimisant les coûts doit satisfaire à deux conditions :

  1. Il est sur l'isoquante y ;
  2. aucun autre point sur l'isoquante y est sur une droite d'isocoût inférieure.

Le cas des isoquantes convexes lisses par rapport à l'origine

Si l'isoquante y est lisse et convexe par rapport à l'origine et le panier qui minimise les coûts implique un montant positif de chaque facteur de production, alors à un panier de facteurs de production minimisant les coûts un isocoût est tangent à l'isoquante y. Or, puisque la valeur absolue de la pente de la droite d'isocoût est le rapport des coûts d'intrant , et la valeur absolue de la pente d'une isoquante est le taux marginal de substitution technique (TMST), nous arrivons à la conclusion suivante : Si les isoquantes sont lisses et convexes à l'origine et le panier de facteurs de production qui minimise les coûts implique un montant positif de chaque facteur de production, alors ce panier satisfait aux deux conditions suivantes :

  • Il est sur l'isoquante y (ex. : f(K, L) = y, où f est la fonction de production) ;
  • le TMST au (K, L) est égale à w/r.

La condition que le TMST est égale à w/r peut être donnée à l'interprétation intuitive suivante. On sait que le TMST est égal au rapport des produits marginaux des deux facteurs de production. Donc la condition que les TMST soient égaux au rapport du coût d'intrant est équivalente à la condition que le produit marginal par dollar est égal pour les deux facteurs de production. Cette condition est logique : à une combinaison de facteur de production particulière, si un dollar supplémentaire dépensé sur le facteur 1 produit plus de rendement qu'un dollar supplémentaire dépensé sur le facteur 2, alors il doit être utilisé plus de facteur 1 et moins de facteur 2, et donc que la combinaison de facteur de production peut ne pas être optimale. Seulement si un dollar dépensé sur chaque facteur est également productive, c'est le panier de facteurs de production optimale.

Références
  1. Hervé Defalvard, Fondements de la microéconomie : Les choix individuels, vol. 1, Bruxelles, De Boeck Supérieur, coll. « Questions d'économie et de gestion », , 190 p. (ISBN 978-2-8041-3993-3, lire en ligne).
  2. Johanna Etner et Meglena Jeleva, Microéconomie, vol. 1, Dunod, coll. « Openbook », , 368 p. (ISBN 978-2-10-071404-9, lire en ligne).
  3. Frédéric Aprahamian, André Bertrand, Damien Besancenot, Jean-Baptiste Ferrari et Kim Huynh, Microéconomie, Rosny, Bréal, coll. « Grand Amphi », , 384 p. (ISBN 978-2-7495-0749-1, lire en ligne).
  • Portail de l’économie
  • Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.