Jet de Landau-Squire

Lignes de courant d'un jet de Landau-Squire pour c = 0.01

Lignes de courant d'un jet de Landau-Squire pour c = 0.1

Lignes de courant d'un jet de Landau-Squire pour c = 1

Le problème est décrit en coordonnées sphériques  ${\displaystyle (r,\theta ,\phi )}$. La vitesse est  ${\displaystyle \mathbf {v} =(u,v,0)}$. L'équation de conservation de quantité de mouvement pour un écoulement incompressible s'écrit

${\displaystyle {\begin{aligned}&{\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}(r^{2}u)+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(v\sin \theta )=0\\[8pt]&u{\frac {\partial u}{\partial r}}+{\frac {v}{r}}{\frac {\partial u}{\partial \theta }}-{\frac {v^{2}}{r}}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial r}}+\nu \left(\nabla ^{2}u-{\frac {2u}{r^{2}}}-{\frac {2}{r^{2}}}{\frac {\partial v}{\partial \theta }}-{\frac {2v\cot \theta }{r^{2}}}\right)\\[8pt]&u{\frac {\partial v}{\partial r}}+{\frac {v}{r}}{\frac {\partial v}{\partial \theta }}+{\frac {uv}{r}}=-{\frac {1}{\rho r}}{\frac {\partial p}{\partial \theta }}+\nu \left(\nabla ^{2}v+{\frac {2}{r^{2}}}{\frac {\partial u}{\partial \theta }}-{\frac {v}{r^{2}\sin ^{2}\theta }}\right)\end{aligned}}}$

où

${\displaystyle \nabla ^{2}={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)}$

Les conditions limites à l'infini amont sont

${\displaystyle u=v=0\,,\quad p=p_{\infty }}$

On recherche une solution sous forme d'un écoulement auto-similaire

${\displaystyle u={\frac {\nu }{r\sin \theta }}f'(\theta ),\quad v=-{\frac {\nu }{r\sin \theta }}f(\theta )}$

En introduisant cet ansatz dans l'équation ci-dessus il vient

${\displaystyle {\frac {p-p_{\infty }}{\rho }}=-{\frac {v^{2}}{2}}+{\frac {\nu u}{r}}+{\frac {c_{1}}{r^{2}}}}$

${\displaystyle -{\frac {u^{2}}{r}}+{\frac {v}{r}}{\frac {\partial u}{\partial \theta }}={\frac {\nu }{r^{2}}}\left[2u+{\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial u}{\partial \theta }}\right)\right]+{\frac {2c_{1}}{r^{3}}}}$

où  ${\displaystyle c_{1}}$  est une constante.

On effectue le changement de variable  ${\displaystyle \mu =\cos \theta }$. Les composantes de la vitesse s'écrivent

${\displaystyle u=-{\frac {\nu }{r}}f'(\mu ),\quad v=-{\frac {\nu }{r}}{\frac {f(\mu )}{\sqrt {1-\mu ^{2}}}}}$

L'équation de conservation devient

${\displaystyle f'^{2}+ff''=2f'+[(1-\mu ^{2})f'']'-2c_{1}}$

Après une double intégration

${\displaystyle f^{2}=4\mu f+2(1-\mu ^{2})f'-2(c_{1}\mu ^{2}+c_{2}\mu +c_{3})}$

où  ${\displaystyle c_{2}}$  et ${\displaystyle c_{3}}$  sont des constantes d'intégration.

Il s'agit là d'une équation de Riccati dont la solution est

${\displaystyle f=\alpha (1+\mu )+\beta (1-\mu )+{\frac {2(1-\mu ^{2})(1+\mu )^{\beta }}{(1-\mu )^{\alpha }}}\left[c-\int _{1}^{\mu }{\frac {(1+\mu )^{\beta }}{(1-\mu )^{\alpha }}}\right]^{-1}}$

où  ${\displaystyle \alpha ,\ \beta ,\ c}$  sont des constantes. La solution ne peut admettre de singularité qu'à l'origine[4]. On a donc  ${\displaystyle \alpha =\beta =0}$  où, de manière équivalente  ${\displaystyle c_{1}=c_{2}=c_{3}=0}$. Dès lors

${\displaystyle f={\frac {2(1-\mu ^{2})}{c+1-\mu }}={\frac {2\sin ^{2}\theta }{c+1-\cos \theta }}}$

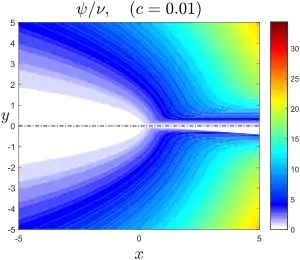
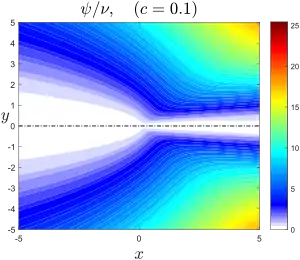
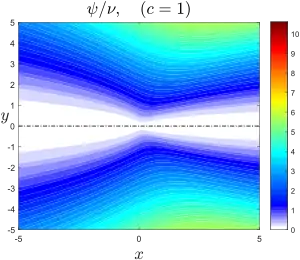
${\displaystyle f}$  est reliée à la fonction de courant par  ${\displaystyle \psi =\nu rf}$. Ses contours se confondent donc avec celles-ci. Cette solution décrit l'écoulement entraîné en amont écarté de l'axe par la source dont l'intensité est donnée par la constante c qui s'interprète en termes de force volumique axiale[4]. Le « bord » du jet peut être défini par le point où les lignes de courant sont le plus près de l'axe, soit

${\displaystyle \theta _{o}=\arccos \left({\frac {1}{1+c}}\right)}$

On voit que

${\displaystyle c\to \infty \quad \Rightarrow \quad \theta _{0}\to {\frac {\pi }{2}}}$

La limite correspond au jet de Schlichting dans lequel la source constitue un véritable mur pour l'écoulement amont.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Landau–Squire jet » (voir la liste des auteurs).

• Portail de la physique