Lemme des bergers
En mathématiques, le lemme des bergers, ou principe des bergers[1] est une propriété combinatoire.
Ne doit pas être confondu avec Lemme de Berge.
Il peut s'énoncer au niveau élémentaire par :
Lemme des bergers — Si un ensemble E possède une partition en p sous-ensembles contenant chacun r éléments, alors E contient p × r éléments.
L'appellation « lemme des bergers » provient de la situation suivante : un berger ne voyant que les pattes de ses moutons pourra déterminer le nombre d'animaux en divisant le nombre de pattes par quatre[2].
On peut utiliser ce lemme si on connaît le nombre d'éléments de E, un des nombres p et r étant connu mais pas l'autre, on en déduit celui des nombres p et r qu'on ne connaissait pas : il suffit de diviser le nombre d'éléments de E par p ou r suivant les cas.
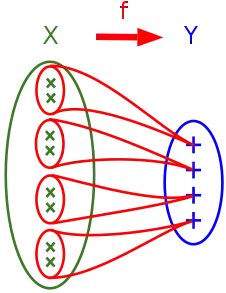
Une version plus abstraite et plus générale de ce principe s'énonce comme suit, en désignant par f -1( { y } ) l'ensemble des antécédents d'un élément y par une application f :
Principe des bergers[1] — Étant donnés deux ensembles quelconques X et Y, de cardinaux respectifs a et b, et une surjection f : X → Y telle que les ensembles f -1( { y } ), pour y élément de Y, aient tous même cardinal c, alors on a a = b × c.
Note et référence
- N. Bourbaki, Éléments de mathématique : Théorie des ensembles [détail des éditions], partie III, § 5, no 8, proposition 9, p. III.41, aperçu sur Google Livres.
- J.-P. Marco et al., Mathématiques L1: Cours complet avec fiches de révision, Pearson, (lire en ligne), p. 98.
Articles connexes
- Indice d'un sous-groupe
- Formule du produit (théorie des groupes)
- Combinaison
- Arrangement
- Espace vectoriel fini
- Principe des tiroirs
- Portail des mathématiques