Lieu planckien

En physique et en colorimétrie, le lieu plankien (ou lieu de Planck, ou encore lieu du corps noir) est la trajectoire (ou lieu géométrique) que suit la couleur d'un corps noir incandescent dans un diagramme de chromaticité donné. Cette trajectoire part du rouge profond, passe par l’orange, le jaune, le blanc, et s'achève dans le bleu à très hautes températures.

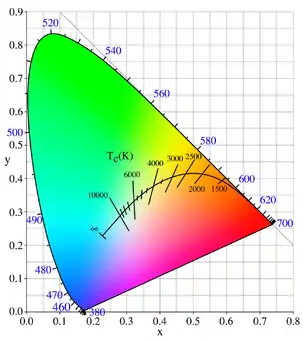
Lieu planckien dans le diagramme de chromaticité de l'espace CIE RGB.

Un espace de couleur est un espace tridimensionnel, c'est-à-dire qu'une couleur y est spécifiée par trois nombres (les coordonnées X, Y et Z de l'espace CIE RGB de 1931, par exemple ; ou tout autre système comme « teinte, saturation, luminance »), qui permettent de spécifier la couleur et la brillance d'un stimulus visuel donné. Le diagramme de chromaticité est une projection à deux dimensions de cette représentation, obtenue en éliminant la luminance. L'espace CIE RGB transforme ainsi par projection ses trois coordonnées X, Y et Z en deux coordonnées de chromaticité notées x et y, conduisant au diagramme de chromaticité de la figure ci-contre. C'est généralement dans un tel diagramme de chromaticité qu'est représenté le lieu de Planck.

Inversement, la projection d'un point du diagramme de chromaticité sur ce lieu de Planck détermine la température de couleur de ce point.

Calcul
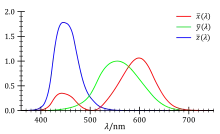
Fonctions colorimétriques de l'observateur CIE 2° de référence x(λ), y(λ) et z(λ).

La représentation du lieu de Planck dans un espace de couleur s'appuie sur les fonctions colorimétriques qui lui sont associées.

Dans l'espace CIE XYZ, par exemple, les trois coordonnées définissant la couleur d'une émission lumineuse sont définies par[1] :

où M(λ,T) est l'exitance de l'émission lumineuse d'un corps noir de température T pour la longueur d'onde λ ; et X(λ), Y(λ) et Z(λ) sont les fonctions colorimétriques (représentées sur le diagramme ci-contre) représentant la sensibilité suivant chacun de ses trois récepteurs de l'observateur de référence en fonction de la longueur d'onde λ.

Le lieu de Planck est alors déterminé en substituant dans l'équation précédente la formule qui donne le spectre de la luminance énergétique spectrale du corps noir, laquelle suit la loi de Planck :

où

  • ν est la fréquence du rayonnement du corps noir, en s−1 ;
  • λ = λ0/n, avec λ0 la longueur d'onde du rayonnement du corps noir dans le vide et n l'indice de réfraction du milieu, est la longueur d'onde du rayonnement du corps noir dans le milieu, en m ;
  • h = 6,626 070 15 × 10−34 J s est la constante de Planck ;
  • c = c0/n, avec c0 = 299 792 458 m s−1 la vitesse de la lumière dans le vide et n l'indice de réfraction du milieu, est la vitesse de propagation du rayonnement du corps noir dans le milieu ;
  • k = 1,380 649 × 10−23 J K−1 est la constante de Boltzmann ;
  • T est la température de la surface du corps noir, en K.

L'intégration de ces équations donne alors les trois coordonnées du lieu de Planck dans l'espace CIE XYZ.

Représentation dans l'espace de chromaticité

Si ces coordonnées sont notées XT, YT et ZT, les coordonnées dans l'espace de chromaticité s'en déduiront par les formules :

Le facteur de la formule, qui dimensionne la luminance énergétique de la source, s'élimine dans l'espace de chromaticité, qui ne dépend que de la couleur.

Paramétrage en mired
Iisothermes en kelvins.
Isothermes en mired.

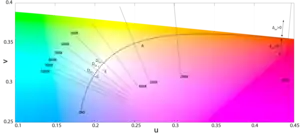
Le lieu de Planck dans l'espace xy correspond à la courbe représentée dans le diagramme de chromaticité ci-dessus. Il est bien entendu possible de calculer point par point les coordonnées de cette courbe en utilisant les formules ci-dessus, mais il est plus rapide dans les applications pratiques d'utiliser une formule approximative. Pour une telle approximation, il est usuel d'utiliser comme paramètre le mired, fonction inverse de la température, parce que le déplacement du point représentatif est plus régulier suivant ce paramètre qu'il ne l'est suivant la température absolue.

Approximation dans l'espace CIE XYZ

Kim et al. utilisent comme approximation une spline cubique[2],[3] :

Les trois spline d'approximation de Kim et al.

Approximation dans l'espace CIE UVW

Le lieu planckien peut également être approximé dans l'espace CIE UVW par l'expression suivante[4]

Cette approximation donne de bons résultats, avec des écarts dans l'intervalle et , pour des températures dans l'intervalle .

Notes et références
  1. (en) Wyszecki, Günter et Stiles, Walter Stanley, Color Science : Concepts and Methods, Quantitative Data and Formulae, Wiley-Interscience, , 2e éd. (ISBN 0-471-39918-3)
  2. Brevet US 7024034 Kim et al., Color Temperature Conversion System and Method Using the Same, 2006-04-04
  3. (en) Bongsoon Kang, Ohak Moon, Changhee Hong, Honam Lee, Bonghwan Cho and Youngsun Kim, « Design of Advanced Color Temperature Control System for HDTV Applications », Journal of the Korean Physical Society, vol. 41, no 6,‎ , p. 865–871 (lire en ligne)
  4. (en) Michael P. Krystek, « An algorithm to calculate correlated colour temperature », Color Research & Application, vol. 10, no 1,‎ , p. 38–40 (DOI 10.1002/col.5080100109) :
    « A new algorithm to calculate correlated colour temperature is given. This algorithm is based on a rational Chebyshev approximation of the Planckian locus in the CIE 1960 UCS diagram and a bisection procedure. Thus time-consuming search procedures in tables or charts are no longer necessary. »

Voir aussi

Articles connexes

Lien externe
  • Portail de la physique
  • Portail des couleurs
  • Portail de la photographie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.