Lissage exponentiel
Le lissage exponentiel est une méthode empirique de lissage et de prévision de données chronologiques affectées d'aléas. Comme dans la méthode des moyennes mobiles, chaque donnée est lissée successivement en partant de la valeur initiale. Le lissage exponentiel donne aux observations passées un poids décroissant exponentiellement avec leur ancienneté. Le lissage exponentiel est une des méthodes de fenêtrage utilisées en traitement du signal. Elle agit comme un filtre passe-bas en supprimant les fréquences élevées du signal initial.
La série de données brutes est notée , commençant à . Le résultat du lissage exponentiel est noté ; celui-ci peut être vu comme une estimation de , débarrassé des aléas (en traitement du signal, on dit du bruit) en fonction du passé. Le résultat dépend cependant de la pratique de l'utilisateur (choix du facteur de lissage).
Le lissage exponentiel n'a vraiment d'intérêt que pour des données à peu près stationnaires (c'est-à-dire qui ne sont pas affectées de fortes croissances ou décroissances ou de variations saisonnières). Lorsqu'il existe une tendance, on doit compliquer la méthode (lissage exponentiel double). Elle n'apporte aucune aide pour le traitement des données saisonnalisées. De caractère empirique, la méthode ne fournit pas d'indications sur les propriétés statistiques des résultats.
Pour une série commençant à , le résultat du lissage exponentiel simple est donné par les formules suivantes :
- pour :
- où est le facteur de lissage, avec
Lissage exponentiel simple
Le fenêtrage exponentiel ou lissage exponentiel simple est attribué à Poisson[1] qui aurait généralisé des méthodes utilisées dès le xviie siècle ; cette méthode fut adoptée par les spécialistes de traitement du signal dans les années 1940.
L'expression la plus élémentaire du lissage exponentiel simple est donnée par l'expression :
La méthode est applicable quand on dispose de deux valeurs brutes ou plus.
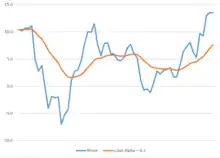
Le paramètre α est un facteur de lissage compris entre 0 et 1. En d'autres termes, st peut être vu comme une moyenne pondérée entre la valeur actuelle yt et la valeur lissée précédente st – 1. Le nom « facteur de lissage » donné à α est trompeur dans la mesure où le lissage diminue quand α augmente et que, dans le cas limite où α = 1, la série lissée est identique à la série brute.
Les valeurs de α proches de 1 réduisent l'incidence du passé et donnent plus de poids aux valeurs récentes ; inversement, les valeurs proches de 0 augmentent le lissage et réduisent l'incidence des valeurs récentes. Il n'y a pas de méthode générale pour déterminer la « bonne valeur » de α. Celle-ci résulte de l'expérience de l'analyste. On peut, dans certains cas, choisir la valeur de α qui minimise la quantité (st – yt )2 (minimisation des carrés de l'erreur de prévision).
Contrairement à d'autres méthodes, le lissage exponentiel ne nécessite pas un nombre minimum de données pour être appliqué (la méthode fonctionne dès la seconde donnée disponible). Toutefois, un « bon » lissage ne sera obtenu qu'après qu'un certain nombre de données aient été lissées ; par exemple, il faudra environ 3/α données bruitées d'un signal constant pour que celui-ci soit approché à 95 %. Contrairement à la moyenne mobile, le lissage exponentiel ne supporte pas les données manquantes.
Techniquement, le lissage exponentiel est un processus ARIMA (en) de classe (0, 1, 1) sans constante[2].
Constante de temps
La constante de temps d'un lissage exponentiel est le temps nécessaire pour que la réponse lissée d'un signal constant atteigne 1 – 1/e ≃ 63% du signal. Cette constante de temps τ est liée au facteur de lissage α par la relation :
où ΔT est la durée de l'intervalle d'échantillonnage des données discrètes. Si cette durée est petite par rapport à la constante de temps, cette expression se simplifie en :
- .
Choix de la valeur initiale
Le lissage exponentiel démarre en posant que s0 = x0. On suppose donc que la première valeur lissée est égale à la première valeur brute observée. Si α est petit, les valeurs lissées dépendent fortement du passé ; la valeur initiale s0 peut donc influer fortement sur les valeurs suivantes. Le choix de la valeur de démarrage du processus de lissage est donc important. On peut, par exemple, retenir comme valeur initiale du lissage la moyenne des dix valeurs précédentes (ou plus ou moins selon la nature des données brutes). Plus est petit, plus les résultats obtenus dépendent des valeurs initiales.
Optimisation
Les résultats du lissage exponentiel dépendent du choix du paramètres de lissage α. Le lissage exponentiel est une méthode empirique et le choix de ce paramètre dépend souvent de l'expérience et des connaissances de l'analyste. On peut toutefois se fonder sur des considérations plus objectives, liées aux données, pour déterminer le « meilleur α » :
- Chaque nouvelle valeur lissée st est une « prévision » de yt.
On obtient la meilleure prévision (au sens des moindres carrés) en recherchant la valeur de qui minimise la somme des carrés des écarts (SCE):
Toutefois, contrairement à la régression linéaire où les paramètres minimisant SCE sont obtenus en résolvant des équation linéaires, les équations à résoudre ici ne sont pas linéaires : on doit donc estimer α avec un algorithme de minimisation.
Pourquoi ce lissage est-il « exponentiel » ?
Le terme « exponentiel » décrit les poids qui sont affectés aux valeurs passées dans l'évaluation de la valeur actuelle : comme
on obtient, en substituant st – 1 par sa valeur :
et en continuant les substitutions :
Le poids des données dans l'évaluation de la valeur actuelle décroit en raison géométrique de leur ancienneté par rapport à la valeur actuelle, c'est-à-dire selon une fonction exponentiellement décroissante.
Comparaison avec la moyenne mobile
Comme le lissage par moyenne mobile, le lissage exponentiel introduit dans les résultats un délai qui dépend de la période d’échantillonnage des données. Dans le lissage par moyenne mobile, on peut compenser cet effet en décalant les valeurs lissées d'une valeur égale à la moitié de la largeur de la fenêtre de lissage (pour une fenêtre de lissage symétrique). Ceci n'est pas possible avec le lissage exponentiel. Du point de vue du calcul, une moyenne mobile n'exige de conserver en mémoire que les k dernières valeurs (pour un fenêtrage de largeur k) alors que le lissage exponentiel nécessite de conserver toutes les valeurs passées.
Lissage exponentiel double
Le lissage exponentiel simple ne donne pas de bons résultats lorsque les données brutes présentent une tendance ou des tendances. Les valeurs lissées présentent une sous-estimation ou une sur-estimation systématique selon le sens de la tendance. Les méthodes de lissage exponentiel double ont pour objet de lisser le niveau des données (c'est-à-dire d'éliminer les variations aléatoires) et de lisser la tendance, c'est-à-dire d'éliminer l'effet de la tendance sur les valeurs lissées.
Il existe deux méthodes de lissage exponentiel double, la méthode de Holt (en)[3] étendue par Winters[4] et la méthode de Brown (en)[5]
Méthode de Holt-Winters
Les données commencent au temps t = 0 ; de nouveau {yt} est la série des données brutes. On dispose au moins des données y0 et y1. Le terme st est la série des valeurs lissées et {σt } les estimations de la tendance.
pour t > 1 :
Le choix de la valeur initiale y0 est une question de pratique ; on peut prendre comme point de départ une moyenne d'un certain nombre de valeurs passées précédentes.
À partir de la période t, une prévision à la période t + m est donnée par :
Méthode de Brown
À partir des données initiales y0 et y1, on calcule :
la valeur lissée pour t ≥ 1 est :
et l'estimation de la tendance :
Application du lissage exponentiel
Le lissage exponentiel simple, double ou même triple a été beaucoup utilisé en traitement analogique du signal. Cette méthode est aussi beaucoup utilisée, de façon empirique pour les prévisions de ventes, la gestion des stocks, etc. Aussi bien pour le traitement du signal numérique qu'en matière de modélisation et de prévision, des méthodes moins empiriques, mais exigeant plus de calcul sont apparues depuis les années 1970. Pour la modélisation et la prévision, les modèles ARIMA (en), plus généraux et mieux fondés théoriquement incluent implicitement le lissage exponentiel.
Mise en œuvre logicielle
- Langage R : Méthode de Holt-Winters dans la bibliothèque stats[6] et la fonction ets dans la bibliothèque forecast[7] (mise en œuvre complète conduisant à de meilleurs résultats[8]).
- IBM SPSS comporte : les lissages simple et saisonnalisé, la méthode à tendance de Holt, la tendance amortie, la méthode de Winters pour les tendances additive et multiplicative dans l'extension Modeler statistical/Time-Series modeling procedure.
- Stata : commande tssmooth[9]
- LibreOffice 5.2[10]
- Microsoft Excel 2016[11]
Voir aussi
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Exponential smoothing » (voir la liste des auteurs).
- Alan V. Oppenheim et Ronald W. Schafer, Digital Signal Processing, Upper Saddle River, N. J., États-Unis, Prentice Hall, , 585 p. (ISBN 0-13-214635-5), p. 5.
- (en) « Averaging and Exponential Smoothing Models » (consulté le ).
- (en) Charles C. Holt, « Forecasting Trends and Seasonals by Exponentially Weighted Averages », Carnegie Institute of Technology, Pittsburgh Office of Naval Research memorandum, no 52, .
- (en) Peter R. Winters, « Forecasting Sales by Exponentially Weighted Moving Averages », Management Science, vol. 6, no 3, , pp. 324-342 (lire en ligne, consulté le ).
- (en) Robert G. Brown, Exponential Smoothing for Predicting Demand, Cambridge, Massachusetts (États-Unis), Arthur D. Little Inc., (lire en ligne).
- « R: Holt-Winters Filtering », sur stat.ethz.ch (consulté le )
- « ets {forecast} | inside-R | A Community Site for R », sur www.inside-r.org (consulté le )
- (en-US) « Comparing HoltWinters() and ets() », sur Hyndsight, (consulté le )
- Documentation de la commande tssmooth de Stata
- (en) « LibreOffice 5.2 : Release Notes - The Document Foundation Wiki », sur documentfoundation.org (consulté le ).
- « Excel Forecasting Functions / Real Statistics Using Excel », sur real-statistics.com (consulté le ).
Bibliographie
- R. Bourbonnais et J.-C. Usunier, La prévision des ventes, Economica, , 6e éd..
Articles connexes
- Portail du temps
- Portail des mathématiques
- Portail des probabilités et de la statistique