Loi bêta

Dans la théorie des probabilités et en statistiques, la loi bêta est une famille de lois de probabilités continues, définies sur $[0,1]$ , paramétrée par deux paramètres de forme, typiquement notés $α$ et $β$ . C'est un cas spécial de la loi de Dirichlet, avec seulement deux paramètres.

Loi bêta
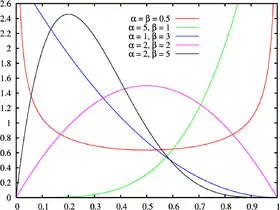Densité de probabilité


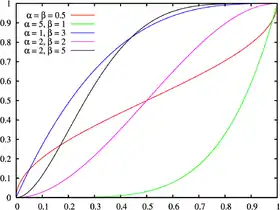Fonction de répartition

Paramètres	$\alpha >0$ forme (réel) $\beta >0$ forme (réel)
Support	$x\in [0;1]\!$
Densité de probabilité	${\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}\!$
Fonction de répartition	$I_{x}(\alpha ,\beta )\!$
Espérance	${\frac {\alpha }{\alpha +\beta }}\!$
Mode	${\frac {\alpha -1}{\alpha +\beta -2}}\!$ pour $\alpha >1,\beta >1$
Variance	${\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}\!$
Asymétrie	$2\,{\frac {(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}$
Kurtosis normalisé	$6\,{\tfrac {(\beta -\alpha )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}\!$
Fonction génératrice des moments	${\displaystyle {}_{1}F_{1}(\alpha$ = $\sum _{k=0}^{\infty }\left({\frac {\mathrm {B} (\alpha +k,\beta )}{\mathrm {B} (\alpha ,\beta )}}\right){\frac {t^{k}}{k!}}$
Fonction caractéristique	${\displaystyle {}_{1}F_{1}(\alpha$

Admettant une grande variété de formes, elle permet de modéliser de nombreuses distributions à support fini. Elle est par exemple utilisée dans la méthode PERT.

Caractérisation

Fonction de densité

La densité de probabilité de la loi bêta est :

f(x;\alpha ,\beta )={\begin{cases}\displaystyle {\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\int _{0}^{1}u^{\alpha -1}(1-u)^{\beta -1}\,du}}&{\hbox{ pour }}x\in [0,1]\\0&{\hbox{ sinon }}\end{cases}}

={\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\;1\!\!1_{[0,1]}(x)

={\frac {1}{\mathrm {B} (\alpha ,\beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\;1\!\!1_{[0,1]}(x)

où $Γ$ est la fonction gamma et $1\!\!1_{[0,1]}$ est la fonction caractéristique de $[0; 1]$ . La fonction bêta $Β$ apparaît comme une constante de normalisation, permettant à la densité de s'intégrer à l'unité.

Fonction de répartition

La fonction de répartition est

F(x;\alpha ,\beta )={\frac {\mathrm {B} _{x}(\alpha ,\beta )}{\mathrm {B} (\alpha ,\beta )}}=I_{x}(\alpha ,\beta )\!

où $\mathrm {B} _{x}(\alpha ,\beta )$ est la fonction bêta incomplète et $I_{x}(\alpha ,\beta )$ est la fonction bêta incomplète régularisée.

Propriétés

Moments

La fonction génératrice des moments est ${\displaystyle {}_{1}F_{1}(\alpha$ .

(Aussi notée ${\displaystyle {}M(\alpha$ . Remplacer $t$ par $it$ pour le fonction caractéristique.) Voir Fonction hypergéométrique confluente.

Formes

La densité de la loi bêta peut prendre différentes formes selon les valeurs des deux paramètres:

$\alpha <1,\ \beta <1$ est en forme de U (graphe rouge);
$\alpha <1,\ \beta \geq 1$ $\text{[math]}$ ou $\alpha =1,\ \beta >1$ $\text{[math]}$ est strictement décroissant (graphe bleu);
- $\alpha =1,\ \beta >2$ est strictement convexe;
- $\alpha =1,\ \beta =2$ est une droite;
- $\alpha =1,\ 1<\beta <2$ est strictement concave;
$\alpha =1,\ \beta =1$ est la loi uniforme continue;
$\alpha =1,\ \beta <1$ $\text{[math]}$ ou $\alpha >1,\ \beta \leq 1$ $\text{[math]}$ est strictement croissant (graphe vert);
- $\alpha >2,\ \beta =1$ est strictement convexe;
- $\alpha =2,\ \beta =1$ est une droite;
- $1<\alpha <2,\ \beta =1$ est strictement concave;
$\alpha >1,\ \beta >1$ est unimodal (graphes noir et violet).

Qui plus est, si $\alpha =\beta$ alors la densité est symétrique autour de 1/2 (graphes rouge et violet).

Généralisations

La loi bêta peut se généraliser en :

la loi bêta décentrée en introduisant un paramètre λ qui décale la moyenne,
la loi bêta rectangulaire en "mélangeant" une loi bêta et une loi uniforme continue,
la loi bêta prime en étendant son support en ]0,∞[.
la loi de Dirichlet généralise la loi bêta en dimension supérieure.

Estimation des paramètres

Soit la moyenne empirique

{\bar {x}}={\frac {1}{N}}\sum _{i=1}^{N}x_{i}

et

v={\frac {1}{N}}\sum _{i=1}^{N}(x_{i}-{\bar {x}})^{2}

la variance. La méthode des moments fournit les estimations suivantes :

\alpha ={\bar {x}}\left({\frac {{\bar {x}}(1-{\bar {x}})}{v}}-1\right),

\beta =(1-{\bar {x}})\left({\frac {{\bar {x}}(1-{\bar {x}})}{v}}-1\right).

Distributions associées

Si $X$ a une distribution bêta, alors la variable aléatoire $T={\frac {X}{1-X}}$ est distribuée selon la loi bêta prime.
La loi bêta-binomiale est la loi conjuguée de la loi bêta.
Si $X\sim \operatorname {U} (0,1)$ où $U$ est la loi uniforme continue, alors $X^{r}\sim \operatorname {Beta} (1/r,1)\$ (pour tout $r>0$ ).
Si $X\sim \operatorname {Beta} (\alpha ,1)$ , alors $-\ln(X)\sim \operatorname {Exp} (\alpha )$ où $\operatorname {Exp}$ est la loi exponentielle.
Si $X$ et $Y$ sont indépendamment distribués selon une loi Gamma, de paramètres $(\alpha ,\theta )$ et $(\beta ,\theta )$ respectivement, alors la variable aléatoire ${\frac {X}{X+Y}}$ est distribuée selon une loi $\mathrm {Beta} (\alpha ,\beta )$ .
La k-ème statistique d'ordre d'un n-échantillon de lois uniformes $\operatorname {U} (0,1)\,$ suit la loi $\operatorname {Beta} (k,n-k+1)\$ .
La loi $\operatorname {Beta} (1/2,1/2)$ est appelée loi arc sinus.
La loi bêta peut s'interpréter comme marginale d'une loi de Dirichlet. En effet, si $(X_{1},\dots ,X_{n})\sim \operatorname {Dirichlet} (\alpha _{1},\dots ,\alpha _{n})$ alors $X_{i}\sim \operatorname {Beta} \left(\alpha _{i},\sum _{k=1}^{n}\alpha _{k}-\alpha _{i}\right).$

Exemple d'occurrence de la loi bêta

La loi bêta apparaît naturellement dans une expérience d'urnes, donnée par George Pólya dans un article de 1930, Sur quelques points de la théorie des probabilités[1]. Il décrit l'expérience suivante : on se donne une urne contenant initialement $r$ boules rouges et $b$ boules bleues, on tire une boule dans l'urne, puis on la remet dans l'urne avec une deuxième boule de même couleur. Alors la proportion de boules rouges tend vers une variable aléatoire de loi $Βeta(r,b)$ , et, inversement, la proportion de boules bleues tend vers une variable aléatoire de loi $Βeta(b,r)$ .

Ce processus étudié par Pólya est ce que l'on appelle aujourd'hui un processus renforcé.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Beta distribution » (voir la liste des auteurs).

George Pólya, « Sur quelques points de la théorie des probabilités », Annales de l'Institut Henri Poincaré,‎ 1930, p. 150 (lire en ligne, consulté le 5 décembre 2018)

Voir aussi

Liens externes

(en) Beta Distribution par Fiona Maclachlan, Wolfram Demonstrations Project, 2007
(en) Beta Distribution – Overview and Example, xycoon.com
(fr) Article de Gearge Polya, "Sur quelques points de la théorie des probabilité, archive de l'institut Henri Poincaré, numdam.org
(en) Beta Distribution, brighton-webs.co.uk

Portail des probabilités et de la statistique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] George Pólya, « Sur quelques points de la théorie des probabilités », Annales de l'Institut Henri Poincaré,‎ 1930, p. 150 (lire en ligne, consulté le 5 décembre 2018)