Loi de Wien
La loi du rayonnement de Wien caractérise la dépendance du rayonnement du corps noir à la longueur d'onde. Il s'agit d'une formule empirique proposée par Wilhelm Wien, qui rend compte de la loi du déplacement de Wien.
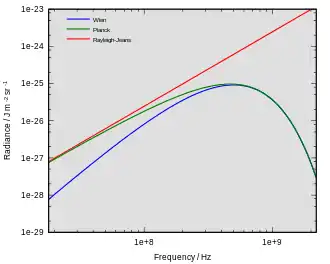
Description
Dans sa forme donnée par Wien en 1896, elle s'écrit :
avec
- : exitance énergétique monochromatique
- λ : longueur d'onde
- C ≈ 3,742 × 10−16 m4 kg s−3 (première constante de rayonnement) ;
- c ≈ 0,014 39 m K (constante de rayonnement) ;
- T : température en kelvin (K).
Cette loi décrit effectivement la présence d'un maximum de rayonnement, mais, contrairement à la Loi de Planck, elle fournit des valeurs fausses pour les grandes longueurs d'onde. En outre, elle implique que l'intensité de rayonnement soit limitée avec l'augmentation de la température, ce que contredit également l'expérience.
Max Planck remédia à cela en 1900, en proposant la formule suivante :
avec
Planck remplaça les constantes empiriques C et c par des constantes naturelles : la constante de Boltzmann, la vitesse de la lumière dans le vide et une nouvelle constante h nommée constante de Planck.
Pour la "petite histoire", la constante h introduite par Planck arrivait comme "ad hoc" sans aucune interprétation physique et c'est Einstein dès 1905 qui, identifiant la variation de l'entropie d'un Gaz Parfait, "solution diluée", avec celle d'un rayonnement monochromatique de densité suffisamment faible, supposa naturellement l'existence "d'atome de lumière". Sur cette hypothèse, celle des quanta lumineux, Planck et tous ses suiveurs mirent plus de 20 ans (1922-1923) à reconnaître sa validité (à cause de la théorie EM de Maxwell), allant même entre-temps jusqu'à congratuler Einstein pour toutes ses contributions à la Physique, mais en excluant la folle idée de ses quanta, comme l'exception qui confirme la règle: S'il est donc nécessaire de cerner un quelconque initiateur sérieux de "début physique" de la mécanique quantique, c'est bien à Einstein qu'il conviendrait de l'identifier, et surtout pas Planck.
Une version simplifiée de la Loi de Wien peut s'exprimer ainsi dans le Système international d'unités :
, avec en Kelvin et en mètres.
Notes et références
- (de) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en allemand intitulé « Wiensches Strahlungsgesetz » (voir la liste des auteurs).
Voir aussi
Articles connexes
Liens externes
- (de) Max Planck, « On an Improvement of Wien’s Equation for the Spectrum » in Verhandlungen der Deutschen physikalischen Gesellschaft, 2, 1900, no 13, p. 202-204.
- Portail de la physique
- Portail de l’énergie