Maximum régularisé

En mathématiques, un maximum régularisé (smooth maximum) d'une famille indicée $x 1, ..., x n$ de nombres est une approximation lisse de la fonction maximum $max(x 1,..., x n)$ , soit une famille paramétrée de fonctions $m α (x 1,..., x n)$ telle que la fonction $m α$ est régulière pour toute valeur réelle de $α$ , et tend vers la fonction maximum pour $α \to \infty$ . Le concept de minimum régularisé peut être défini de façon similaire. Dans plusieurs cas, une famille peut servir à approcher les deux fonctions, le maximum pour des valeurs positives très grandes, le minimum vers l'infini négatif :

m_{\alpha }\to \max \ {\textrm {pour}}\ \alpha \to \infty ,\ m_{\alpha }\to \min \ {\textrm {pour}}\ \alpha \to -\infty .

Le terme peut être utilisée pour toute fonction régularisante se comportant de façon similaire à la fonction maximum, sans être paramétrée.

Exemples

Maximum régularisé appliqué aux fonctions

-x

et

x

pour plusieurs valeurs de coefficients. On voit que la fonction est très lisse pour

α = 0,5

et plus raide pour

α = 8

.

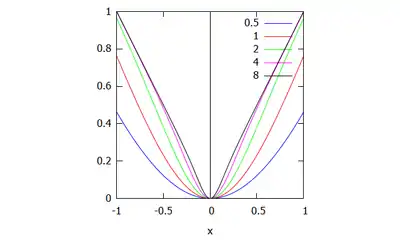
Pour de grandes valeurs du paramètre $α > 0$ , la fonction $S α$ définie ci-après, parfois appelée « $α$ -softmax », est une approximation lisse et différentiable de la fonction maximum. Pour des valeurs négatives du paramètre grandes en valeur absolue, elle approche le minimum. La fonction $α$ -softmax est définie par[1] :

S_{\alpha }(x_{1},\ldots ,x_{n})={\frac {\sum _{i=1}^{n}x_{i}\mathrm {e} ^{\alpha x_{i}}}{\sum _{i=1}^{n}\mathrm {e} ^{\alpha x_{i}}}}

$S α$ a les propriétés suivantes :

$S_{\alpha }{\underset {\alpha \to +\infty }{\longrightarrow }}\max$
$S 0$ renvoie la moyenne arithmétique
$S_{\alpha }{\underset {\alpha \to -\infty }{\longrightarrow }}\min$

Le gradient de $S α$ est lié à la fonction softmax et vaut

\nabla _{x_{i}}S_{\alpha }(x_{1},\ldots ,x_{n})={\frac {\mathrm {e} ^{\alpha x_{i}}}{\sum _{j=1}^{n}\mathrm {e} ^{\alpha x_{j}}}}[1+\alpha (x_{i}-S_{\alpha }(x_{1},\ldots ,x_{n}))].

Ceci rend la fonction softmax intéressante pour des techniques d'optimisation utilisant la descente de gradient.^{[réf. souhaitée]}

Normes de Hölder

Une forme de maximum régularisé peut être basé sur une moyenne généralisée. Par exemple, pour des valeurs $x 1, ..., x n$ positives, on peut utiliser une moyenne d'ordre $α > 1$ , soit

S_{\alpha }(x_{1},\ldots ,x_{n})=\left({\frac {1}{n}}\sum _{j=1}^{n}x_{j}^{\alpha }\right)^{\frac {1}{\alpha }}.

LogSumExp

Un autre maximum régularisé est connu sous le nom « LogSumExp »:

\mathrm {LSE} (x_{1},\ldots ,x_{n})=\ln(\exp(x_{1})+\ldots +\exp(x_{n}))

La fonction peut être normalisée si les $x i$ sont tous positifs, menant à une fonction définie sur $[0 , +\infty[n$ vers $[0 , +\infty[$ :

g(x_{1},\ldots ,x_{n})=\ln(\exp(x_{1})+\ldots +\exp(x_{n})-(n-1))

Le terme $(n - 1)$ est un coefficient de correction pour prendre en compte que $exp(0) = 1$ , assurant ainsi qu'on ait bien $g (0, ... ,0) = 0$ si tous les $x i$ sont nuls.

La fonction LogSumExp peut être paramétré pour éviter les artefacts de lissage. On appelle cette forme « $α$ -quasimax », définie par[1]:

{\mathcal {Q}}_{\alpha }(x_{1},\ldots ,x_{n})={\frac {1}{\alpha }}\mathrm {LSE} (\alpha x_{1},\ldots ,\alpha x_{n})={\frac {1}{\alpha }}\ln(\exp(\alpha x_{1})+\ldots +\exp(\alpha x_{n}))

Utilisation dans des méthodes numériques

Les maximums lisses ont un intérêt dans les recherches d'extrema sur des ensembles de données discrètes[2] ou des algorithmes d'optimisation par descente du gradient.

Voir aussi

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Smooth maximum » (voir la liste des auteurs).

(en) M. Lange, D. Zühlke, O. Holz et T. Villmann, « Applications of l_p-norms and their smooth approximations for gradient based learning vector quantization », Proc. ESANN,‎ 2014, p. 271-276 (lire en ligne)
(en) Gabor Takacs, « Smooth maximum based algorithms for classification, regression, and collaborative filtering », Acta Technica Jaurinensis, vol. 3, n^o 1,‎ 2010, p. 27-63

Portail de l'analyse

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[ESANN-1] (en) M. Lange, D. Zühlke, O. Holz et T. Villmann, « Applications of l_p-norms and their smooth approximations for gradient based learning vector quantization », Proc. ESANN,‎ 2014, p. 271-276 (lire en ligne)

[2] (en) Gabor Takacs, « Smooth maximum based algorithms for classification, regression, and collaborative filtering », Acta Technica Jaurinensis, vol. 3, n^o 1,‎ 2010, p. 27-63