Meigu Guan
Meigu Guan (chinois : 管梅谷, aussi romanisé en Mei-Ko Kwan ou Mei-ku Kuan, né en 1934 à Shanghai) est un mathématicien et chercheur chinois qui « est devenu l'un des principaux experts de l'optimisation mathématique en Chine »[1]. Il est connu pour ses recherches sur le problème du postier chinois, et a été le président de la Shandong Normal University (en).

| Naissance | |
|---|---|
| Formation | |
| Activités |
| A travaillé pour |
|---|
Contributions à la recherche
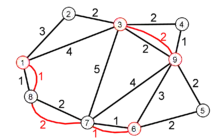
Guan est connu pour la formulation du problème du postier chinois[1]. Ce problème algorithmique est une généralisation du problème de la promenade d'Euler, dans lequel l'entrée est un graphe à arêtes pondérées et le but est de trouver un cycle de poids total minimum qui permet de visiter chaque arête du graphe au moins une fois. Les applications de ce problème comprennent des problèmes de planification des transports tels que la planification des itinéraires pour une flotte de chasse-neiges pour nettoyer toutes les rues d'une ville, en un temps total minimum[2].
Guan a travaillé comme chargé de cours à la Shandong Normal University (en) pendant le Grand Bond en avant de 1958 à 1960, période au cours de laquelle les mathématiciens chinois ont été encouragés à travailler sur des problèmes pratiques. Il a publié ses travaux sur ce problème, alors appelé « problème d'inspection des routes », en 1960, et son livre a été traduit en anglais en 1962[1]. Il a attiré l'attention de Jack Edmonds, qui a donné au problème son autre nom, le « problème du postier chinois », en l'honneur de Guan[3],[4] et a prouvé que ce problème peut être résolu de manière optimale en temps polynomial.
L'une des contributions ultérieures de Guan a été de prouver que, en revanche, le « problème du postier dans le vent » est NP-complet; c'est une version généralisée du problème du postier dans lequel le coût de la traversée d'une arête dépend de la direction dans laquelle elle est parcourue[5].
Carrière universitaire
Guan achève ses études en 1957 à l'Université normale de la Chine de l'Est de Shanghai, et la même année, il rejoint le corps professoral de la Shandong Normal University[6]. Il a servi en tant que président de la Shandong Normal University de 1984 à 1990. Il est ensuite devenu directeur du département de recherche opérationnelle à l'Université Fudan de 1990 à 1995, date après laquelle il est parti à l'école de commerce de l'Institut royal de technologie de Melbourne en Australie[1].
Sélection de publications
- (zh) Mei-ko Kwan, « Graphic programming using odd or even points », Acta Mathematica Sinica (en), vol. 10, , p. 263–266 (Math Reviews 0162630, lire en ligne). Traduit en Chinois, Mathématiques 1, American Mathematical Society, 1962, pp. 273-277.
- (zh) Meigu Guan et Handing Zheng, Linear Programming, Shandong Science and Technology Press, .
- Meigu Guan, « On the windy postman problem », Discrete Applied Mathematics, vol. 9, no 1, , p. 41–46 (DOI 10.1016/0166-218X(84)90089-1, Math Reviews 754427).
- Meigu Guan, Graph theory and its applications: East and West (Jinan, 1986), vol. 576, New York, New York Academy of Sciences, (DOI 10.1111/j.1749-6632.1989.tb16400.x, Math Reviews 1110817), p. 203–218.
Références
- Martin Grötschel et Ya-xiang Yuan, « Euler, Mei-Ko Kwan, Königsberg, and a Chinese postman », Documenta Mathematica, vol. Extra, , p. 43–50 (Math Reviews 2991468, lire en ligne).
- Marcus Woo, « The mathematics behind getting all that damned snow off your street », Wired, (lire en ligne).
- Grötschel & Yuan (2012). Des sources créditent Alan J. Goldman (en) d'avoir suggéré ce nom à Edmonds ; voir par exemple « Chinese postman problem », dans Vreda Pieterse et Paul E. Black, Dictionary of Algorithms and Data Structures, National Institute of Standards and Technology, (lire en ligne).
- Douglas B. West, « Introduction to Graph Theory », 2001, Prentice-Hall.
- Guan (1984)
- Martin Grötschel, Beijing Block Course "Combinatorial Optimization at Work", Institute of Computational Mathematics and Scientific/Engineering Computing of Chinese Academy of Sciences, (lire en ligne).
Liens externes
- Portail des mathématiques
- Portail de la Chine